题目内容
4.已知等比数列{an}的前n项和为Sn,且Sn=qn+r(n∈N*,q>0且q≠1),则实数r的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
分析 根据数列通项公式和前n项和公式的关系求出数列的通项公式,利用a1满足an进行求解即可.
解答 解:当n≥2时,an=Sn-Sn-1=qn+r-(qn-1+r)=qn-qn-1=(q-1)qn-1,
当n=1时,a1=S1=q+r,
∵{an}是等比数列,
∴a1满足an=(q-1)qn-1,
即q+r=q-1,
则r=-1,
故选:D
点评 本题主要考查等比数列通项公式的求解,利用关系n≥2时,an=Sn-Sn-1是解决本题的关键.注意要验证当n=1时是否成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知椭圆的焦点在y轴上,若椭圆$\frac{x^2}{2}+\frac{y^2}{2m}=1$的离心率为$\frac{1}{2}$,则m的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{3}$ |
13.某校为提高教师课堂教学效率,在每个教室安装了多媒体白板系统,若此多媒体白板系统使用的年限x(年)与所支出的维修费用y(万元)有下列统计资料数表:
根据上表可得回归方程为$\hat y$=1.23x+$\hat a$,由此可以估计该多媒体白板系统使用年限为10年的维修费用约为( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | 10.38 | B. | 12.38 | C. | 13.08 | D. | 13.28 |
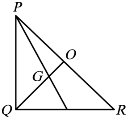 如图,△PQR中,∠Q=90°,又∠QPR=45°,已知G为△PQR的重心,若OG=a,求△PQR的周长(用a表示).
如图,△PQR中,∠Q=90°,又∠QPR=45°,已知G为△PQR的重心,若OG=a,求△PQR的周长(用a表示).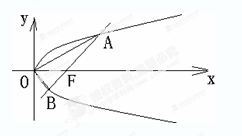 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.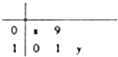 有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )
有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )