题目内容
【题目】定义一种运算ab= ![]() ,令f(x)=(3x2+6x)(2x+3﹣x2),则函数f(x)的最大值是 .
,令f(x)=(3x2+6x)(2x+3﹣x2),则函数f(x)的最大值是 .
【答案】4
【解析】解:∵ab= ![]() ,
,
∴f(x)=(3x2+6x)(2x+3﹣x2)= 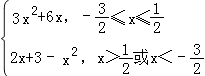 ,
,
当﹣ ![]() ≤x≤
≤x≤ ![]() 时,f(x)=3x2+6x=3(x+1)2﹣3,
时,f(x)=3x2+6x=3(x+1)2﹣3,
可得f(x)在x=﹣1处取得最小值﹣3;在x= ![]() 处取得最大值
处取得最大值 ![]() ;
;
当x> ![]() 或x<﹣
或x<﹣ ![]() 时,f(x)=﹣x2+2x+3=﹣(x﹣1)2+4,
时,f(x)=﹣x2+2x+3=﹣(x﹣1)2+4,
当x=1时,f(x)取得最大值4.
综上可得,f(x)的最大值为4.
所以答案是:4.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如表所示:
年份 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
利润x | 12.2 | 14.6 | 16 | 18 | 20.4 | 22.3 |
支出y | 0.62 | 0.74 | 0.81 | 0.89 | 1 | 1.11 |
根据统计资料,则( )
A.利润中位数是16,x与y有正线性相关关系
B.利润中位数是18,x与y有负线性相关关系
C.利润中位数是17,x与y有正线性相关关系
D.利润中位数是17,x与y有负线性相关关系