题目内容
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过点P作圆C的切线,切点为A、B.记四边形PACB的面积为f(P),当P(x0,y0)在圆D:(x+4)2+(y-1)2=4上运动时,f(P)的取值范围为
[2
,4
]
| 2 |
| 3 |
[2
,4
]
.| 2 |
| 3 |
分析:根据题意画出相应的图形,连接CD并延长,与圆D分别交于M、N,由圆C与圆D的方程得出圆心C、D的坐标,即各自的半径r与R,利用两点间的距离公式求出圆心距|CD|的长,当P在N处时,四边形ACBP面积最小;当P在M处时,四边形ACBP面积最大,分别求出即可得到f(P)的范围.
解答: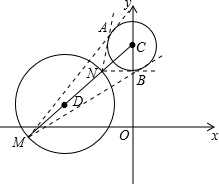 解:由题意得到圆心C(0,4),半径r=1;圆心D(-4,1),半径R=2,
解:由题意得到圆心C(0,4),半径r=1;圆心D(-4,1),半径R=2,
∴|CD|=
=5,
∴|CN|=5-2=3,|CM|=5+2=7,
当P位于图形中的N位置时,四边形ACBP面积最小,
过P作圆C的切线,切点分别为A、B,连接AC,BC,可得出|AC|=|BC|=1,且CA⊥AP,CB⊥BP,
在Rt△ACP中,根据勾股定理得:AP=
=2
,
此时S四边形ACBP=2S△ACP=AP•AC=2
;
当P位于图形中的M位置时,四边形ACBP面积最大,
同理得到S四边形ACBP=4
,
综上,f(P)的范围为[2
,4
].
故答案为:[2
,4
]
 解:由题意得到圆心C(0,4),半径r=1;圆心D(-4,1),半径R=2,
解:由题意得到圆心C(0,4),半径r=1;圆心D(-4,1),半径R=2,∴|CD|=
| (-4-0)2+(1-4)2 |
∴|CN|=5-2=3,|CM|=5+2=7,
当P位于图形中的N位置时,四边形ACBP面积最小,
过P作圆C的切线,切点分别为A、B,连接AC,BC,可得出|AC|=|BC|=1,且CA⊥AP,CB⊥BP,
在Rt△ACP中,根据勾股定理得:AP=
| 32-12 |
| 2 |
此时S四边形ACBP=2S△ACP=AP•AC=2
| 2 |
当P位于图形中的M位置时,四边形ACBP面积最大,
同理得到S四边形ACBP=4
| 3 |
综上,f(P)的范围为[2
| 2 |
| 3 |
故答案为:[2
| 2 |
| 3 |
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两点间的距离公式,以及勾股定理,利用了数形结合的思想,数形结合思想是数学中重要的思想方法,做题时注意灵活运用.

练习册系列答案
相关题目
 已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)