题目内容
【题目】实数x，y满足 
，
（1）若z=2x+y，求z的最大值；
（2）若z=x2+y2 ， 求z的取值范围．
【答案】
（1）解：由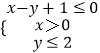 
，
作出可行域如图中阴影部分所示
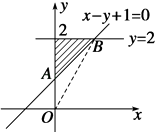
z=2x+y令z=0画出y=﹣2x，由图知， 
，可得B（1，2），
当z=2x+y经过点B（1，2）时，zmax=4
（2）解：z=x2+y2表示可行域内的任意一点与坐标原点之间的距离的平方．
因此x2+y2的范围最小为|OA|2（取不到），最大为|OB|2．
，得A（0，1），∴|OA|2=（ 
）2=1，|OB|2=（ 
）2=5．
∴z的最大值为5，没有最小值．故z的取值范围是（1，5]
【解析】画出约束条件的可行域，（1）利用目标函数的几何意义求解即可．（2）利用目标函数的几何意义，可行域内的点到原点的距离的平方，观察求解即可、
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
