题目内容

【题目】已知抛物线，不与坐标轴垂直的直线与抛物线交于两点，当且时，.

（1）求抛物线的标准方程；

（2）若过定点，点关于轴的对称点为，证明：直线过定点，并求出定点坐标.

【答案】（1）（2）见解析，定点.

【解析】

（1）根据直线和抛物线的相交的弦长公式建立方程即可求出抛物线的标准方程.
（2）根据对称性设出，的坐标，联立方程求出直线的方程，结合方程进行判断即可.

（1）将抛物线方程和直线方程联立，得，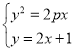

消去得，由根与系数关系可得，，

则，

则，化简得，解之得或（舍去），

故抛物线的标准方程为；

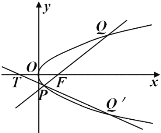
（2）直线方程为，

设坐标分别为.

因为点与点关于轴对称，所以坐标为，显然点也在抛物线上.

设直线与轴交点的坐标为.

由消去得.

所以，.

由于三点共线，则，

从而，化简得，

又，

，

则，

故过定点.

练习册系列答案
相关题目

【题目】已知，是轴正半轴上两点（在的左侧），且，过，作轴的垂线，与抛物线在第一象限分别交于，两点.

（Ⅰ）若，点与抛物线的焦点重合，求直线的斜率；

（Ⅱ）若为坐标原点，记的面积为，梯形的面积为，求的取值范围.

【题目】如图，在直三棱柱中，，，，.

（1）证明：平面；

（2）在线段上是否存在点，使得平面与平面所成的锐二面角为，若存在，求出线段的长度；若不存在，说明理由.

【题目】平面直角坐标系xOy中，已知椭圆C：的离心率为，且点在椭圆C上.椭圆C的左顶点为A.

（1）求椭圆C的方程

（2）椭圆的右焦点且斜率为的直线与椭圆交于P，Q两点，求三角形APQ的面积；

（3）过点A作直线与椭圆C交于另一点B.若直线交轴于点C，且，求直线的斜率.

【题目】已知定义在上的函数.

（1）当时，解不等式；

（2）若对任意恒成立，求的取值范围.

【题目】近年来，在新高考改革中，打破文理分科的“”模式初露端倪，其中语、数、外三门课为必考科目，剩下三门为选考科目选考科目成绩采用“赋分制”，即原始分数不直接用，而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分，假定省规定：选考科目按考生成绩从高到低排列，按照占总体、、、分别赋分分、分、分、分，为了让学生们体验“赋分制”计算成绩的方法，省某高中高一（）班（共人）举行了以此摸底考试（选考科目全考，单料全班排名），知这次摸底考试中的物理成绩（满分分）频率分布直方图，化学成绩（满分分）茎叶图如图所示，小明同学在这次考试中物理分，化学多分．

（1）采用赋分制后，求小明物理成绩的最后得分；

（2）若小明的化学成绩最后得分为分，求小明的原始成绩的可能值；

（3）若小明必选物理，其他两科从化学、生物、历史、地理、政治五科中任选，求小明此次考试选考科目包括化学的概率．

【题目】如图，四棱锥中，平面平面，若，四边形是平行四边形，且.

（Ⅰ）求证：；

（Ⅱ）若点在线段上，且平面，，，求二面角的余弦值.

【题目】已知椭圆的离心率为，分别为椭圆的左，右焦点，直线过点与椭圆交于两点，当直线的斜率为时，线段的长为.

（1）求椭圆的方程；

（2）过点且与直线垂直的直线与椭圆交于两点，求四边形面积的最小值.

【题目】已知函数.

（1）若，求函数的单调性；

（2）若且，求证：.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网