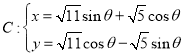题目内容
【题目】已知椭圆![]() :
:![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)求过椭圆的右焦点且倾斜角为135°的直线,被椭圆截得的弦长;
(3)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,求证:直线
的右顶点,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
【答案】(1)椭圆![]() 的方程:
的方程:![]() (2)
(2)![]() (3)见解析,
(3)见解析,![]()
【解析】
(1)根据椭圆短轴长公式和离心率公式进行求解即可;
(2)求出过椭圆的右焦点且倾斜角为135°的直线方程,将与椭圆![]() 方程联立,结合椭圆弦长公式和一元二次方程根与系数关系进行求解即可;
方程联立,结合椭圆弦长公式和一元二次方程根与系数关系进行求解即可;
(3)根据以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,可以得到向量的数量积为零,将直线方程与椭圆方程联立,利用一元二次方程根与系数进行求解即可.
的右顶点,可以得到向量的数量积为零,将直线方程与椭圆方程联立,利用一元二次方程根与系数进行求解即可.
(1)因为椭圆![]() :
:![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() ,
,
所以有![]() 且
且![]() ,而
,而![]() ,解得
,解得![]() ,因此椭圆
,因此椭圆![]() 的标准方程为:
的标准方程为:![]() ;
;
(2)因为![]() ,所以椭圆
,所以椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() ,因此过椭圆的右焦点且倾斜角为135°的直线方程是
,因此过椭圆的右焦点且倾斜角为135°的直线方程是![]() ,
,
因此有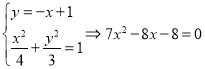 因此设交点坐标分别为
因此设交点坐标分别为![]() ,因此有
,因此有![]() ,因此有
,因此有
![]() ,
,
所以直线被椭圆截得的弦长为![]() ;
;
(3)设![]() ,由题意可知
,由题意可知![]() ,设椭圆右顶点的坐标为:
,设椭圆右顶点的坐标为:![]() ,因为以
,因为以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,所以有
的右顶点,所以有
![]() ,
,
即![]() .
.
直线![]() 与椭圆
与椭圆![]() 的方程联立,得:
的方程联立,得:![]()
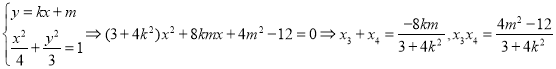 因此
因此![]() ,
,
因此由![]() 可得:
可得:![]() ,化简得:
,化简得:
![]() ,或
,或![]()
当![]() 时,直线
时,直线![]() 方程为
方程为![]() 该直线恒过
该直线恒过![]() 点这与已知矛盾,故舍去;
点这与已知矛盾,故舍去;
当![]() 时,直线
时,直线![]() 方程为
方程为![]() 该直线恒过
该直线恒过![]() 点,综上所述:直线
点,综上所述:直线![]() 过定点
过定点![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】新高考取消文理科,实行“![]() ”模式,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人,并把调查结果制成下表:
”模式,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年,请根据上表完成
称为中老年,请根据上表完成![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: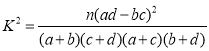 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
【题目】若养殖场每个月生猪的死亡率不超过![]() ,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只3 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001).
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下: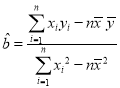 ,
,![]()
参考数据:![]() .
.