题目内容
设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+ ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+
 ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.(1)在(0,+∞)上单调递增.(2)0
(1)函数的定义域为(0,+∞).
f′(x)=ln x+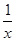 -1,不妨令g(x)=ln x+
-1,不妨令g(x)=ln x+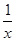 -1,g′(x)=
-1,g′(x)=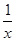 -
-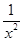 =
= ,
,
当x>1 ,g′(x)>0,函数g(x)=f′(x)单调递增,又因为f′(x)>f′(1)=0,所以x>1,f′(x)>0,函数f(x)单调递增;
当0<x<1,g′(x)<0,g(x)=f′(x)单调递减,
又因为f′(x)>f′(1)=0,所以0<x<1,f′(x)>0.
函数f(x)单调递增.
所以函数y=f(x)在(0,+∞)上单调递增.
(2)h(x)=ln x+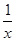 -1+
-1+ ,h′(x)=
,h′(x)=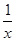 -
-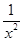 -
- =
=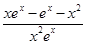 ,设φ(x)=xex-ex-x2,φ′(x)=xex-2x=x(ex-2),当x∈(0,ln 2),φ′(x)<0,函数φ(x)单调递减,
,设φ(x)=xex-ex-x2,φ′(x)=xex-2x=x(ex-2),当x∈(0,ln 2),φ′(x)<0,函数φ(x)单调递减,
又因为φ(x)<φ(0)=-1<0,所以0<x<ln 2,h′(x)<0,函数h(x)单调递减.
当x∈(ln 2,+∞),φ′(x)>0,函数φ(x)单调递增,又因为φ(x)>φ(ln 2)=2ln 2-2-(ln 2)2,又φ(1)=-1<0,φ(2)=e2-4>0,故存在x0∈(1,2),使得φ(x)=0,即x0ex0-ex0- =0,在(0,x0)上,φ(x)<0,在(x0,+∞)上,φ(x)>0.
=0,在(0,x0)上,φ(x)<0,在(x0,+∞)上,φ(x)>0.
即h(x)在(0,x0)上递减,在(x0,+∞)上递增.
所以有h(x)≥h(x0)=ln x0+ -1+
-1+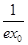 ,又
,又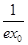 =
= -
- ,所以h(x)≥h(x0)=ln x0+
,所以h(x)≥h(x0)=ln x0+ -1+
-1+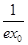 =ln x0+
=ln x0+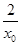 -
- -1,不妨令M(x)=ln x+
-1,不妨令M(x)=ln x+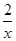 -
-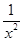 -1,当x∈(1,2)时,M′(x)=
-1,当x∈(1,2)时,M′(x)=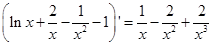 .
.
M′(x)= =
=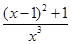 >0恒成立,所以,M(x)是单增函数,又M(1)=0,M(2)=ln 2-
>0恒成立,所以,M(x)是单增函数,又M(1)=0,M(2)=ln 2-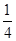 <1,
<1,
所以有1>h(x0)=ln x0+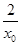 -
- -1>0.
-1>0.
所以k≤0,所以k的最大值为0.
f′(x)=ln x+
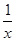 -1,不妨令g(x)=ln x+
-1,不妨令g(x)=ln x+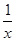 -1,g′(x)=
-1,g′(x)=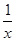 -
-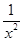 =
= ,
,当x>1 ,g′(x)>0,函数g(x)=f′(x)单调递增,又因为f′(x)>f′(1)=0,所以x>1,f′(x)>0,函数f(x)单调递增;
当0<x<1,g′(x)<0,g(x)=f′(x)单调递减,
又因为f′(x)>f′(1)=0,所以0<x<1,f′(x)>0.
函数f(x)单调递增.
所以函数y=f(x)在(0,+∞)上单调递增.
(2)h(x)=ln x+
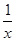 -1+
-1+ ,h′(x)=
,h′(x)=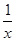 -
-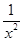 -
- =
=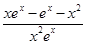 ,设φ(x)=xex-ex-x2,φ′(x)=xex-2x=x(ex-2),当x∈(0,ln 2),φ′(x)<0,函数φ(x)单调递减,
,设φ(x)=xex-ex-x2,φ′(x)=xex-2x=x(ex-2),当x∈(0,ln 2),φ′(x)<0,函数φ(x)单调递减,又因为φ(x)<φ(0)=-1<0,所以0<x<ln 2,h′(x)<0,函数h(x)单调递减.
当x∈(ln 2,+∞),φ′(x)>0,函数φ(x)单调递增,又因为φ(x)>φ(ln 2)=2ln 2-2-(ln 2)2,又φ(1)=-1<0,φ(2)=e2-4>0,故存在x0∈(1,2),使得φ(x)=0,即x0ex0-ex0-
 =0,在(0,x0)上,φ(x)<0,在(x0,+∞)上,φ(x)>0.
=0,在(0,x0)上,φ(x)<0,在(x0,+∞)上,φ(x)>0.即h(x)在(0,x0)上递减,在(x0,+∞)上递增.
所以有h(x)≥h(x0)=ln x0+
 -1+
-1+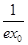 ,又
,又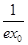 =
= -
- ,所以h(x)≥h(x0)=ln x0+
,所以h(x)≥h(x0)=ln x0+ -1+
-1+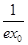 =ln x0+
=ln x0+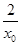 -
- -1,不妨令M(x)=ln x+
-1,不妨令M(x)=ln x+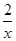 -
-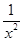 -1,当x∈(1,2)时,M′(x)=
-1,当x∈(1,2)时,M′(x)=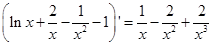 .
.M′(x)=
 =
=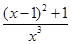 >0恒成立,所以,M(x)是单增函数,又M(1)=0,M(2)=ln 2-
>0恒成立,所以,M(x)是单增函数,又M(1)=0,M(2)=ln 2-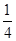 <1,
<1,所以有1>h(x0)=ln x0+
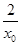 -
- -1>0.
-1>0.所以k≤0,所以k的最大值为0.

练习册系列答案
相关题目
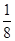 时,证明:方程f(x)=f
时,证明:方程f(x)=f 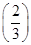 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解. ,
, .
. ,求函数
,求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数 满足
满足 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: .
.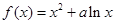 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.  的值;
的值; 根的个数,并证明你的结论;
根的个数,并证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
 的最小值;
的最小值; ,
, .
. 时,
时, 的图象与
的图象与 的图象有唯一的公共点;
的图象有唯一的公共点; 时,
时, 的取值范围.
的取值范围.
 时,求
时,求 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.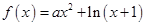 .
.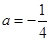 时,求函数
时,求函数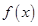 的单调区间;
的单调区间;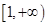 上为减函数,求实数
上为减函数,求实数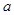 的取值范围;
的取值范围;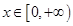 时,不等式
时,不等式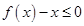 恒成立,求实数
恒成立,求实数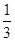 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.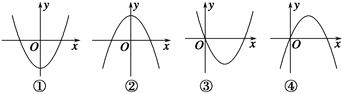
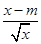 有解,求实数m的取值范围.
有解,求实数m的取值范围.