题目内容
已知函数f(x)=aln x+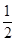 x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.
x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.
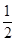 x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.
x2(a>0),若对定义域内的任意x,f′(x)≥2恒成立,则a的取值范围是________.[1,+∞)
由题意得f′(x)=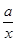 +x≥2
+x≥2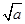 ,当且仅当
,当且仅当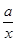 =x,
=x,
即x=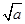 时取等号,
时取等号,
∵f′(x)≥2,∴只要f′(x)min≥2即可,
即2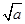 ≥2,解得a≥1.
≥2,解得a≥1.
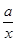 +x≥2
+x≥2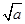 ,当且仅当
,当且仅当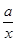 =x,
=x,即x=
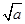 时取等号,
时取等号,∵f′(x)≥2,∴只要f′(x)min≥2即可,
即2
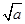 ≥2,解得a≥1.
≥2,解得a≥1.
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
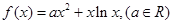
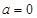 时,求
时,求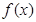 的最小值;
的最小值;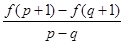 >1恒成立,求实数a的取值范围;
>1恒成立,求实数a的取值范围;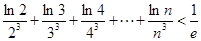 (其中
(其中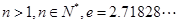 )。
)。 .其中
.其中 .
. 的值;
的值; ,若
,若 ,求
,求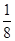 时,证明:方程f(x)=f
时,证明:方程f(x)=f 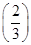 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解.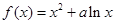 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.  的值;
的值; 根的个数,并证明你的结论;
根的个数,并证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.

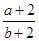 的取值范围是( )
的取值范围是( )
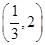
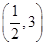
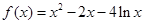 ,则
,则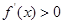 的解集为________.
的解集为________.