题目内容
如图几何体中,四边形ABCD为矩形,AB=3BC=6,EF =4,BF=CF=AE=DE=2, EF∥AB,G为FC的中点,M为线段CD上的一点,且CM =2.
(1)证明:平面BGM⊥平面BFC;
(2)求三棱锥F-BMC的体积V.
详见解析
解析试题分析:(1)连接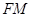 ,由已知可证
,由已知可证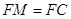 ,
,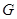 为
为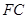 的中点,
的中点,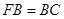 ,所以可证
,所以可证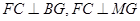 ,即
,即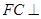 面
面 ,可证面面垂直;
,可证面面垂直;
(2)根据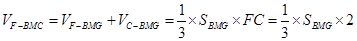 公式,所以中点时求
公式,所以中点时求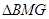 的面积,根据第一问所证,可知
的面积,根据第一问所证,可知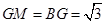 ,
, ,代入面积公式与体积公式,即可求得体积,此题属于中档习题,属于文科考察中点.
,代入面积公式与体积公式,即可求得体积,此题属于中档习题,属于文科考察中点.
试题解析:(1) 连接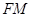
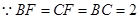 ,
,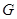 为
为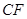 的中点
的中点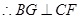 ,
,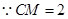 ,
,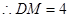 ,
,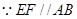 ,
,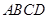 为矩形
为矩形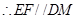 ,又
,又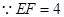 ,
,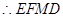 为平行四边形
为平行四边形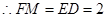 ,
,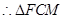 为正三角形
为正三角形 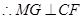 ,
,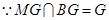
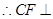 面
面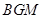 ,
,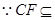 面
面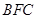 ,
,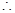 面
面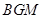
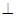 面
面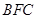 6分
6分
(2)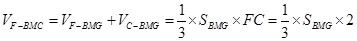 ,
,
因为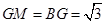 ,
, ,所以
,所以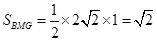 ,所以
,所以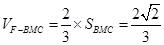 12分
12分
考点:1.面面垂直的判定;2.几何体的体积计算.

练习册系列答案
相关题目
 的菱形
的菱形 沿较短对角线
沿较短对角线 折成二面角
折成二面角 ,点
,点 分别为
分别为 的中点,给出下列四个命题:
的中点,给出下列四个命题: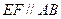 ;②
;② 是异面直线
是异面直线 与
与 ;④
;④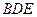 .
. 中,
中, ,
, 平面
平面 ,
, 为
为 的中点,
的中点, ,
, .
. ;
; 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 .
.

 -A BC中,AB
-A BC中,AB  AC, AB=AC=2,
AC, AB=AC=2,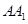 =4,点D是BC的中点.
=4,点D是BC的中点.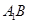 与
与 所成角的余弦值;
所成角的余弦值; 与
与 所成二面角的正弦值.
所成二面角的正弦值.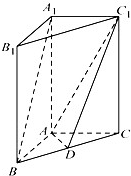

 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.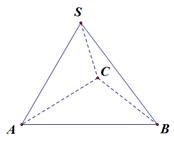
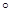 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.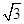 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.