题目内容
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.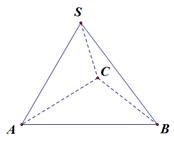
二面角 的余弦值为
的余弦值为 .
.
解析试题分析:先作出二面角的平面角,由面面垂直可得线面垂直,可考虑利用三垂线定理作出二面角的平面角:故可先由题意 作
作 于
于 ,过
,过 作
作 于
于 ,连
,连 ,从而可得
,从而可得 平面
平面 ,又由
,又由 ,故
,故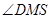 为二面角
为二面角 的平面角,从而问题就转化为求线段
的平面角,从而问题就转化为求线段 与
与 的长度,根据题意易得
的长度,根据题意易得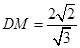 ,
, ,从而
,从而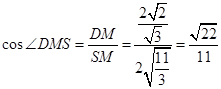 ,即二面角
,即二面角 的余弦值为
的余弦值为 .
.
试题解析:如图,过 作
作 于
于 ,过
,过 作
作 于
于 ,连
,连 ,
,
∵平面 平面
平面 ,∴
,∴ 平面
平面 ,∴
,∴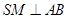 ,
,
又∵ ,∴
,∴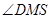 为二面角
为二面角 的平面角,在
的平面角,在 中,
中, ,
,
在 中过
中过 作
作 于
于 ,
,
∵ ,
, ,
, ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
∵ 且
且 ,∴
,∴ ,
,
∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ ,
,
在 中,
中,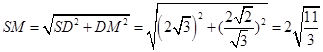 ,
,
∴ ,即二面角
,即二面角 的余弦值为
的余弦值为 .
.
考点:1.面面垂直与线面垂直的转化;2.利用三垂线定理求二面角的平面角大小.

练习册系列答案
相关题目
 ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.

 中,底面
中,底面 是矩形,
是矩形,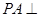 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 的高为
的高为 ,底面
,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点 在底面上的射影是正方形
在底面上的射影是正方形 .
. 是棱
是棱 的中点.试求直线
的中点.试求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 为矩形,平面
为矩形,平面 平面
平面

 问
问 为何值时,四棱锥
为何值时,四棱锥 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 的侧棱
的侧棱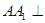 平面
平面 ,
, 为等边三角形,侧面
为等边三角形,侧面 是正方形,
是正方形, 是
是 的中点,
的中点, 是棱
是棱 上的点.
上的点.
 平面
平面 ;
; 时,求正方形
时,求正方形 中,
中,
 、
、 分别为棱
分别为棱 、
、 的中点,则点
的中点,则点 到平面
到平面 的距离为
的距离为