题目内容
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(1)详见解析;(2)
解析试题分析:(1)若 的线
的线 ∥面
∥面 ,且
,且 ,由线面平行的性质定理可知
,由线面平行的性质定理可知 ∥
∥ ,即若证得
,即若证得 ∥
∥ ,则可证得
,则可证得 ∥面
∥面 。由已知可知
。由已知可知 ∥
∥ 且
且 ,则点
,则点 为
为 中点时根据平行四边形可证得
中点时根据平行四边形可证得 ∥
∥ 。(2)设所求的二面角的大小为
。(2)设所求的二面角的大小为 ,则
,则 。(也可用空间向量法)
。(也可用空间向量法)
解法一:以D点为原点建立如图所示的空间直角坐标系,使得 轴和
轴和 轴的正半轴分别经过点A和点E,则各点的坐标为
轴的正半轴分别经过点A和点E,则各点的坐标为 ,
, ,
, ,
, ,
, ,
,
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为 ,∴
,∴
 ,而
,而 是平面ACD的一个法向量,
是平面ACD的一个法向量,
此即证得BF∥平面ACD; 6分
(2)设平面BCE的法向量为 ,则
,则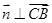 ,且
,且 ,
,
由 ,
, ,
,
∴ ,不妨设
,不妨设 ,则
,则 ,即
,即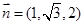 ,
,
∴所求角 满足
满足 ,∴
,∴ ; 13分
; 13分
解法二:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB//ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则
 ,∴
,∴
 ,
,
∴四边形ABFH是平行四边形,∴ ,
,
由 平面ACD内,
平面ACD内, 平面ACD,
平面ACD, 平面ACD
平面ACD
(2)由已知条件可知 即为
即为 在平面ACD上的射影,设所求的二面角的大小为
在平面ACD上的射影,设所求的二面角的大小为 ,则
,则 ,
,
易求得BC=BE ,CE
,CE ,∴
,∴ ,
,
而 ,∴
,∴ ,且
,且 ,∴
,∴
考点:1线线平行、线面平行;2二面角。

练习册系列答案
相关题目


 .
. 平面
平面 .
.

 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
,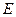 分别是
分别是 的中点,
的中点, .
. ;
; ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
 的侧棱
的侧棱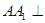 平面
平面 ,
, 为等边三角形,侧面
为等边三角形,侧面 是正方形,
是正方形, 是
是 的中点,
的中点, 是棱
是棱 上的点.
上的点.
 平面
平面 ;
; 时,求正方形
时,求正方形 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 为正方体
为正方体 的点
的点 的个数,并说明理由.
的个数,并说明理由.
 中,
中, ,G是
,G是 上的动点。
上的动点。

 ;
; 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;