题目内容
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥![]() ,二面角
,二面角![]() 为直二面角.
为直二面角.


(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 分别为
分别为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)通过计算证明出二面角![]() 为直二面角,即可证明平面
为直二面角,即可证明平面![]() 平面
平面![]() ;
;
(2)建立空间直角坐标系,利用空间向量法求平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量数量积可得二面角
的法向量,利用向量数量积可得二面角![]() 的余弦值.
的余弦值.
(1)证明:在![]() 中,
中,![]() ,
,
![]()
![]() 为
为![]() 的中点,
的中点,![]() .
.
又![]() ,
,![]() .
.![]() .
.
![]() ,
,![]() .
.
![]() 二面角
二面角![]() 为直二面角,
为直二面角,![]() 平面
平面![]() 平面
平面![]() .
.
![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
可求得![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 分别为
分别为![]() 的中点,
的中点,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
由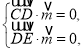 得
得 令
令![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 得
得 令
令![]() ,则
,则![]() .
.
 ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?
【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为
两种不同的数学方式试验甲、乙两个大一新班(人数均为![]() 人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各
人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各![]() 名的高等数学期末考试成绩,得到茎叶图:
名的高等数学期末考试成绩,得到茎叶图:


(1)学校规定:成绩不得低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考方式:![]() ,其中
,其中![]() )
)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.30C.35D.40



