题目内容
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
在平行四边形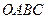 中,已知过点
中,已知过点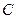 的直线与线段
的直线与线段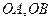 分别相交于点
分别相交于点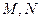 。若
。若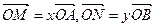 。
。
(1)求证: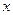 与
与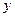 的关系为
的关系为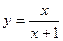 ;
;
(2)设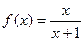 ,定义在
,定义在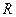 上的偶函数
上的偶函数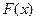 ,当
,当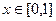 时
时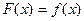 ,且函数
,且函数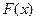 图象关于直线
图象关于直线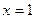 对称,求证:
对称,求证: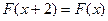 ,
, 并求
并求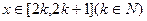 时的解析式;
时的解析式;
(3)在(2)的条件下,不等式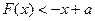 在
在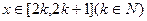 上恒成立,求实数
上恒成立,求实数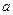 的取值范围。
的取值范围。
在平行四边形
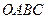 中,已知过点
中,已知过点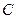 的直线与线段
的直线与线段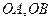 分别相交于点
分别相交于点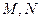 。若
。若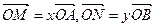 。
。(1)求证:
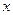 与
与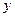 的关系为
的关系为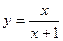 ;
;(2)设
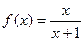 ,定义在
,定义在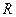 上的偶函数
上的偶函数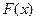 ,当
,当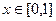 时
时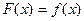 ,且函数
,且函数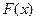 图象关于直线
图象关于直线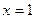 对称,求证:
对称,求证: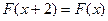 ,
, 并求
并求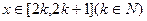 时的解析式;
时的解析式;
(3)在(2)的条件下,不等式
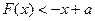 在
在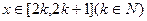 上恒成立,求实数
上恒成立,求实数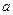 的取值范围。
的取值范围。略
(1)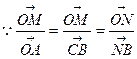 ,…………………………………………2分
,…………………………………………2分
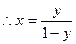 ,从而
,从而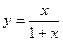 。…………………………………………………4分
。…………………………………………………4分
(2)当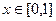 时,
时,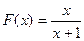 。
。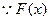 图像关于直线
图像关于直线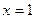 对称,
对称,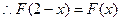 ,
,
…………………………………………………………5分
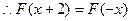 ,又
,又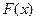 为偶函数,
为偶函数,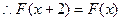 。
。
…………………………………………………………7分
设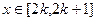 ,则
,则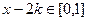 ,………………………………………8分
,………………………………………8分
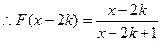 ,即
,即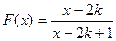 。
。
…………………………………………………………10分
(3)不等式为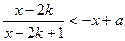 ,…………………………………………12分
,…………………………………………12分
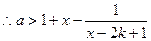 对
对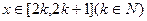 恒成立,因此
恒成立,因此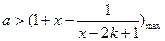 。…………………………………………………………14分
。…………………………………………………………14分
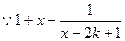 在
在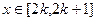 上单调递增,
上单调递增,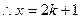 时其最大值为
时其最大值为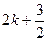 ,
,
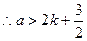 ,即
,即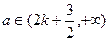
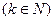 。……………………………………16分
。……………………………………16分
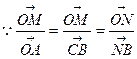 ,…………………………………………2分
,…………………………………………2分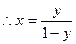 ,从而
,从而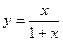 。…………………………………………………4分
。…………………………………………………4分(2)当
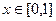 时,
时,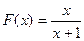 。
。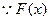 图像关于直线
图像关于直线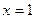 对称,
对称,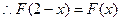 ,
,…………………………………………………………5分
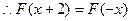 ,又
,又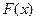 为偶函数,
为偶函数,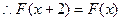 。
。…………………………………………………………7分
设
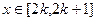 ,则
,则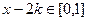 ,………………………………………8分
,………………………………………8分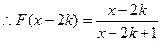 ,即
,即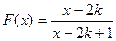 。
。…………………………………………………………10分
(3)不等式为
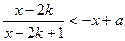 ,…………………………………………12分
,…………………………………………12分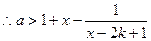 对
对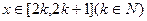 恒成立,因此
恒成立,因此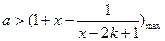 。…………………………………………………………14分
。…………………………………………………………14分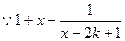 在
在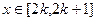 上单调递增,
上单调递增,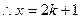 时其最大值为
时其最大值为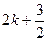 ,
,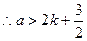 ,即
,即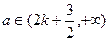
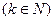 。……………………………………16分
。……………………………………16分
练习册系列答案
相关题目
 ,
, ,定义函数f(x)=
,定义函数f(x)= 。
。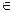 R时求函数f(x)的最大值及此时的x值。
R时求函数f(x)的最大值及此时的x值。 |a-kb| (k>0).
|a-kb| (k>0).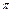 ,b=
,b= ,求a·b的最大值及相应的x值.
,求a·b的最大值及相应的x值. 、
、 、
、 ,其中
,其中 与
与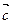 的夹角为
的夹角为 ,
, 的夹角为
的夹角为 ,
, ,并且
,并且
 的值.
的值.
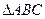 所在平面内一点,若
所在平面内一点,若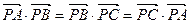 ,则P是
,则P是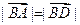 ,当E点在线段AD上移动时,若
,当E点在线段AD上移动时,若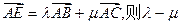 的最大值是( )
的最大值是( )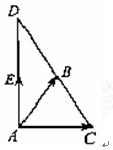
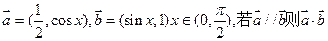 =" " ( )
=" " ( )


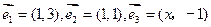 ,
, ,则实数
,则实数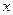 的值是 .
的值是 . ,
,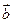 =
=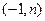 .若
.若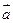 与
与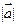 等于
等于