题目内容
一个三角形数表按如下方式构成(如图:其中项数 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: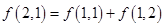 ;
;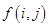 为数表中第
为数表中第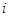 行的第
行的第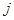 个数.
个数.
求第2行和第3行的通项公式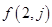 和
和 ;
;
证明:数表中除最后2行外每一行的数都依次成等差数列,并求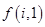 关于
关于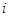 (
(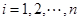 )的表达式;
)的表达式;
(3)若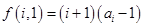 ,
,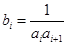 ,试求一个等比数列
,试求一个等比数列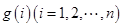 ,使得
,使得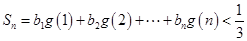 ,且对于任意的
,且对于任意的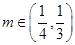 ,均存在实数
,均存在实数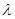 ?,当
?,当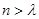 时,都有
时,都有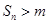 .
.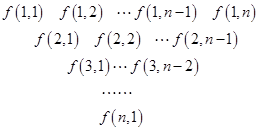
(1) ,
, ;(2)证明见解析,
;(2)证明见解析, ;(3)
;(3) .
.
解析试题分析:(1)根据定义, ,因此
,因此

 ,
, ;(2)由于第
;(2)由于第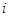 行的数依赖于第
行的数依赖于第 的数,因此我们可用数学归纳法证明,设第
的数,因此我们可用数学归纳法证明,设第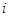 行的公差为
行的公差为 ,
,
 ,而
,而

 ,从而
,从而 ,即
,即 ,于是有
,于是有 ,由此可求得
,由此可求得 ;(3)由(2)得
;(3)由(2)得 ,所以
,所以 ,那么
,那么 可得,
可得,
 ,由于下面要求和,我们把
,由于下面要求和,我们把 变形为
变形为 ,为了能求和
,为了能求和 ,我们可首先取
,我们可首先取 ,这样可得
,这样可得
 ,
, ,且当
,且当
 时,
时, .因此当
.因此当 时,不等式
时,不等式 ,必定有解,取其中一个为
,必定有解,取其中一个为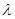 即可.
即可.
试题解析:(1)
 . (3分)
. (3分)
(2)由已知,第一行是等差数列,假设第 行是以
行是以 为公差的等差数列,则由
为公差的等差数列,则由
 (常数)知第
(常数)知第 行的数也依次成等差数列,且其公差为
行的数也依次成等差数列,且其公差为 .综上可得,数表中除最后2行以外每一行都成等差数列; (7分)
.综上可得,数表中除最后2行以外每一行都成等差数列; (7分)
由于 ,所以
,所以 ,所以
,所以 ,由
,由 ,
,
得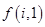
 , (9分)
, (9分)
于是 ,
,
即 ,又因为
,又因为 ,所以,数列
,所以,数列 是以2为首项,1为公差的等差数列, 所以,
是以2为首项,1为公差的等差数列, 所以, ,所以
,所以 (
(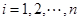 ). (12分)
). (12分)
(3)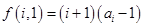
 ,
, ,
,
令
 , (14分)
, (14分)
 . (15分)
. (15分)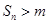

 ,
, 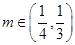
 ,
,

练习册系列答案
相关题目
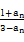 (n∈N*),且a1=
(n∈N*),且a1= .
.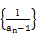 是等差数列,并求an.
是等差数列,并求an.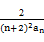 (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn. 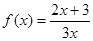 , 数列
, 数列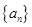 满足
满足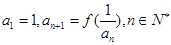 .
.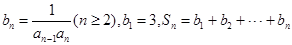 ,若
,若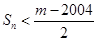 对一切
对一切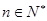 成立,求最小正整数m.
成立,求最小正整数m.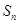 为等差数列
为等差数列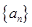 的前
的前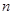 项和,已知
项和,已知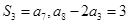 .
.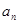 ;
;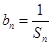 ,数列
,数列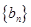 的前
的前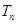 ,求证:
,求证: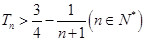 .
. 为等比数列,其前n项和为
为等比数列,其前n项和为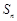 ,且满足
,且满足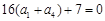 ,
,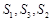 成等差数列.
成等差数列.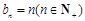 ,记
,记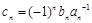 ,求数列
,求数列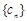 前n项和
前n项和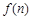 .
.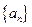 的前
的前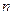 项和为
项和为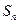 .已知
.已知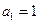 ,
,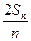 =an+1-
=an+1-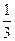 n2-n-
n2-n-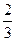 (
(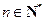 )
)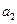 的值;
的值;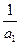 +
+ +…+
+…+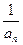 <
<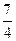 .
.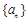 满足
满足 .
.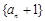 为等比数列,并求出数列
为等比数列,并求出数列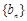 满足
满足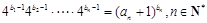 .证明:数列
.证明:数列 .
. }的公差
}的公差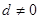 ,
,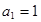 ,且
,且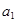 ,
,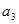 ,
,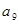 成等比数列.
成等比数列.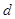 及通项
及通项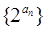 的前
的前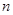 项和
项和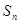 .
.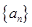 中,
中,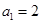 ,
,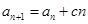 (
(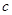 是常数,
是常数,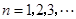 ),且
),且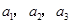 成公比不为
成公比不为 的等比数列.
的等比数列.