题目内容
已知等差数列{ }的公差
}的公差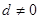 ,
,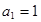 ,且
,且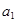 ,
,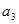 ,
,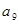 成等比数列.
成等比数列.
(1)求数列{ }的公差
}的公差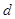 及通项
及通项 ;
;
(2)求数列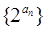 的前
的前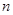 项和
项和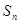 .
.
(1) =n;(2)2n+1-2.
=n;(2)2n+1-2.
解析试题分析:(1)由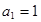 ,
,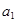 ,
,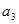 ,
,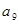 成等比数列得:
成等比数列得: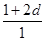 =
=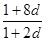 解得d=1,d=0(舍去),即可求出通项公式;
解得d=1,d=0(舍去),即可求出通项公式;
(2)由(1)知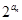 =
=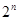 ,由等比数列前n项和公式可求出结果.
,由等比数列前n项和公式可求出结果.
试题解析:解:(1)由题设知公差d≠0,
由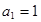 ,
,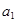 ,
,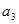 ,
,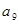 成等比数列得:
成等比数列得: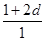 =
=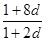 , 3分
, 3分
解得d=1,d=0(舍去) 4分
故{ }的通项
}的通项 =1+(n-1)×1=n. 6分
=1+(n-1)×1=n. 6分
(2)由(1)知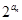 =
=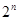 , 8分
, 8分
由等比数列前n项和公式得Sm=2+22+23+ +2n=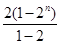 11分
11分
=2n+1-2. 12分
考点:1.等差数列和等比数列的性质;2.等比数列的前n项活动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
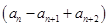 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′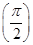 =0.
=0.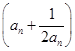 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: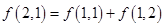 ;
;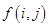 为数表中第
为数表中第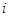 行的第
行的第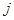 个数.
个数.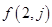 和
和 ;
;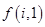 关于
关于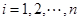 )的表达式;
)的表达式;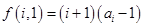 ,
,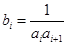 ,试求一个等比数列
,试求一个等比数列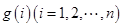 ,使得
,使得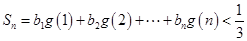 ,且对于任意的
,且对于任意的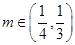 ,均存在实数
,均存在实数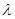 ?,当
?,当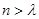 时,都有
时,都有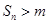 .
.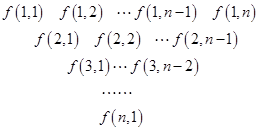
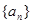 满足
满足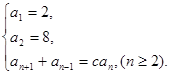 (
(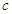 为常数,
为常数,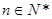 )
)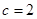 时,求
时,求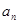 ;
;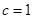 时,求
时,求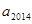 的值;
的值;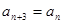 恒成立的常数
恒成立的常数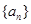 中,已知
中,已知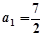 ,
,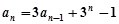 (
(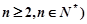 .
.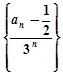 是等差数列;
是等差数列;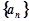 的通项公式
的通项公式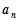 及它的前
及它的前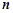 项和
项和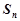 .
.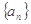 ,等比数列
,等比数列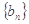 ,满足
,满足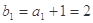 ,
,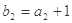 ,
,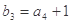 .
.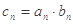 ,求数列{
,求数列{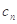 }的前n项和.
}的前n项和.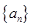 中,
中,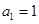 ,对任意的
,对任意的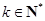 ,
,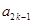 、
、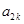 、
、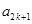 成等比数列,公比为
成等比数列,公比为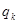 ;
;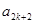 成等差数列,公差为
成等差数列,公差为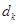 ,且
,且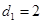 .
.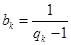 ,求数列
,求数列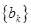 的通项公式;
的通项公式;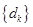 的前
的前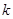 项和
项和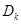 .
.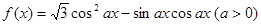 的图像与直线
的图像与直线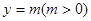 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为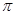 的等差数列.
的等差数列.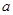 和
和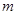 的值;
的值;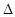 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若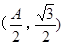 是函数
是函数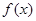 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求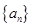 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项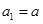 ,
,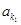 、
、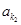 、
、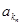 恰为等比数列,且
恰为等比数列,且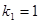 ,
,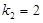 ,
,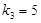 .
.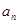 (用
(用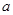 表示);
表示);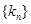 的前
的前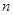 项和为
项和为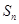 ,求
,求