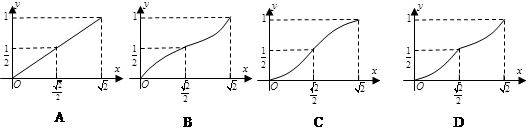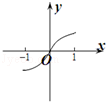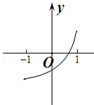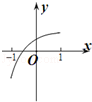题目内容
已知函数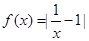 ,若存在正实数
,若存在正实数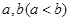 ,使得集合
,使得集合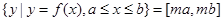 ,则
,则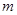 的取值范围为( )
的取值范围为( )
A.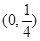 | B.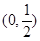 | C.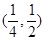 | D.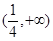 |
A
解析试题分析:由题意,显然m>0,对函数的单调性进行研究知,函数在(-∞,0)上是增函数,在x=0处函数值不存在,在(0,1)函数是减函数,在(1,+∞)函数是增函数,由此结合函数的连续性可以得出ab>0且1∉[a,b].①当b<0时,f(x)在[a,b]上为增函数∴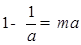 ,
,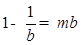
 ,即a,b为方程1?
,即a,b为方程1?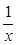 =mx的两根.∴mx2-x+1=0有两个不等的负根 m>0,
=mx的两根.∴mx2-x+1=0有两个不等的负根 m>0,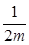 <0,此不等式组无解.②当a≥1时,f(x)在[a,b]上为增函数∴
<0,此不等式组无解.②当a≥1时,f(x)在[a,b]上为增函数∴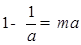 ,
,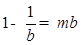 ,即a,b为方程1?
,即a,b为方程1?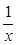 =mx的两根.∴mx2-x+1=0有两个不等的大于1的根.
=mx的两根.∴mx2-x+1=0有两个不等的大于1的根.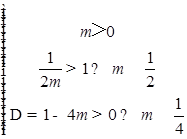 ,解得0<m<
,解得0<m< .③当0<a<b<1时,f(x)在[a,b]上为减函数,∴
.③当0<a<b<1时,f(x)在[a,b]上为减函数,∴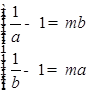 ,两式作差得a=b,无意义.综上,非零实数m的取值范围为(0,
,两式作差得a=b,无意义.综上,非零实数m的取值范围为(0, ).
).
考点:1.函数的单调性及单调区间;2.集合的包含关系判断及应用;3.集合的相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察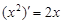 ,
,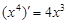 ,
,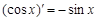 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在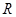 上的函数
上的函数 满足
满足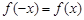 ,记
,记 为
为 的导函数,则
的导函数,则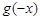 =( )
=( )
A. | B.- | C. | D.- |
没函数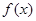 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使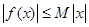 对一切实数x均成 立,则称
对一切实数x均成 立,则称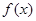 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:①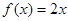 :②
:②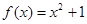 :③
:③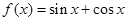 ;④
;④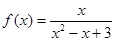 ⑤
⑤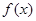 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切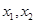 均有
均有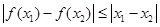 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设a∈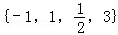 ,则使函数y=xa的定义域是R,且为奇函数的所有a的值是( )
,则使函数y=xa的定义域是R,且为奇函数的所有a的值是( )
| A.1,3 | B.﹣1,1 | C.﹣1,3 | D.﹣1,1,3 |
设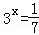 ,则( )
,则( )
| A.﹣2<x<﹣1 | B.﹣3<x<﹣2 |
| C.﹣1<x<0 | D.0<x<1 |
如果函数y=2x+c的图象经过点(2,5),则c=( )
| A.1 | B.0 | C.﹣1 | D.﹣2 |
已知f(x)是R上的奇函数,对x∈R都有f(x+4)=f(x)+f(2)成立,若f(﹣1)=﹣2,则f(2013)等于( )
| A.2 | B.﹣2 | C.﹣1 | D.2013 |
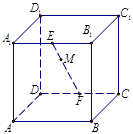
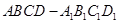 的棱长为
的棱长为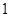 ,
,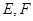 分别是棱
分别是棱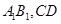 的中点,点
的中点,点 是
是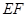 的动点,
的动点,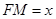 ,过点
,过点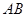 的平面将正方体分成上下两部分,记下面那部分的体积为
的平面将正方体分成上下两部分,记下面那部分的体积为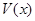 ,则函数
,则函数