题目内容
已知数列{an},其前n项和为Sn.
(1)若对任意的n∈N,a2n﹣1,a2n+1,a2n组成公差为4的等差数列,且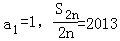 ,求n的值;
,求n的值;
(2)若数列{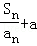 }是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为
}是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为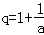
(1)1005
(2)由 +a=(a+1)qn﹣1,可求得Sn=(a+1)qn﹣1an﹣aan,Sn+1=(a+1)qnan+1﹣aan+1,两式相减得(a+1)(1﹣qn)an+1=[a﹣(a+1)qn﹣1]an,若q=1+
+a=(a+1)qn﹣1,可求得Sn=(a+1)qn﹣1an﹣aan,Sn+1=(a+1)qnan+1﹣aan+1,两式相减得(a+1)(1﹣qn)an+1=[a﹣(a+1)qn﹣1]an,若q=1+ ,可证得数列{an}为等比数列,(充分性);若数列{an}为等比数列,可证得q=1+
,可证得数列{an}为等比数列,(充分性);若数列{an}为等比数列,可证得q=1+ ,(必要性).
,(必要性).
解析试题分析:(1)因为a2n﹣1,a2n+1,a2n组成公差为4的等差数列,
所以a2n+1﹣a2n﹣1=4,a2n=a2n﹣1+8(n∈N*),…(2分)
所以a1,a3,a5,…a2n﹣1,a2n+1是公差为4的等差数列,且a2+a4+a6+…+a2n=a1+a3+…+a2n﹣1+8n,…(4分)
又因为a1=1,
所以S2n=2(a1+a3+…+a2n﹣1)+8n
=2[n+ ×4]+8n=4n2+6n=2n(2n+3),
×4]+8n=4n2+6n=2n(2n+3),
所以 =2n+3=2013,所以n=1005.…(6分)
=2n+3=2013,所以n=1005.…(6分)
(2)因为 +a=(a+1)qn﹣1,所以Sn=(a+1)qn﹣1an﹣aan,①
+a=(a+1)qn﹣1,所以Sn=(a+1)qn﹣1an﹣aan,①
所以Sn+1=(a+1)qnan+1﹣aan+1,②
②﹣①,得(a+1)(1﹣qn)an+1=[a﹣(a+1)qn﹣1]an,③…(8分)
(ⅰ)充分性:因为q=1+ ,所以a≠0,q≠1,a+1≠aq,代入③式,得
,所以a≠0,q≠1,a+1≠aq,代入③式,得
q(1﹣qn)an+1=(1﹣qn)an,因为q≠﹣1,q≠1,
所以 =
= ,n∈N*,所以{an}为等比数列,…(12分)
,n∈N*,所以{an}为等比数列,…(12分)
(ⅱ)必要性:设{an}的公比为q0,则由③得(a+1)(1﹣qn)q0=a﹣(a+1)qn﹣1,
整理得(a+1)q0﹣a=(a+1)(q0﹣ )qn,…(14分)
)qn,…(14分)
此式为关于n的恒等式,若q=1,则左边=0,右边=﹣1,矛盾;
若q≠±1,当且仅当 时成立,所以q=1+
时成立,所以q=1+ .
.
由(ⅰ)、(ⅱ)可知,数列{an}为等比数列的充要条件为q=1+ .…(16分)
.…(16分)
考点:等差数列与等比数列的综合
点评:本题考查等差数列与等比数列的综合,考查等差数列的求和与等比数列的分析确定,考查充分必要条件的推理论证,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 中,
中,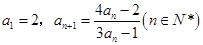 ,设
,设 .
. 的前三项;
的前三项; ;
;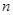 项和为
项和为 ,求证:
,求证: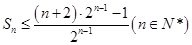 .
. 的各项均为正数,
的各项均为正数,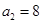 ,
, .
.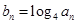 .证明:
.证明: 为等差数列,并求
为等差数列,并求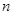 项和
项和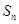 .
. 的前
的前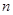 项和为
项和为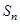 ,且
,且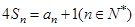 .
. ;(Ⅱ)设
;(Ⅱ)设 ,求数列
,求数列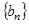 的通项公式。
的通项公式。 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为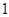 的等比数列.
的等比数列. 的正整数n的最大值
的正整数n的最大值 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且 是
是 与
与 的等差中项
的等差中项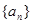 满足:
满足: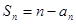 (
(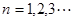 ).
).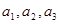 的值;
的值;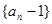 是等比数列;
是等比数列;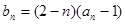 ,
,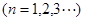 ,如果对任意
,如果对任意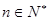 ,都有
,都有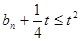 ,
,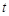 的取值范围.
的取值范围.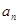 }的前n项和为
}的前n项和为 ,且
,且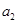 =3,
=3,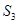 =13,数列{
=13,数列{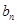 }满足
}满足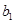 =
=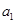 ,点P(
,点P(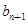 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡. =
=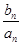 ,数列{
,数列{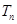 ,若
,若