题目内容
(本小题满分12分)设递增等比数列{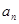 }的前n项和为
}的前n项和为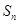 ,且
,且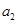 =3,
=3,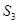 =13,数列{
=13,数列{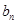 }满足
}满足 =
=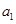 ,点P(
,点P(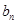 ,
,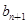 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡.
(Ⅰ)求数列{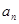 },{
},{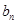 }的通项公式;
}的通项公式;
(Ⅱ)设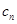 =
=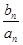 ,数列{
,数列{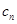 }的前n项和
}的前n项和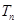 ,若
,若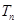 >2a-1恒成立(n∈N﹡),求实数a的取值范围.
>2a-1恒成立(n∈N﹡),求实数a的取值范围.
(1)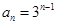 ,
,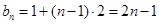 (2)
(2)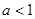
解析试题分析:解:(Ⅰ)由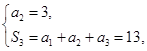 可得
可得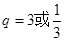 ,
,
因为数列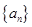 为递增等比数列,所以
为递增等比数列,所以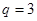 ,
,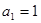 .
.
故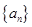 是首项为
是首项为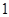 ,公比为
,公比为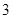 的等比数列. 所以
的等比数列. 所以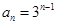 . 3分
. 3分
由点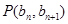 在直线
在直线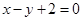 上,所以
上,所以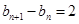 .
.
则数列 是首项为1,公差为2的等差数列.则
是首项为1,公差为2的等差数列.则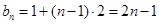 . 5分
. 5分
(Ⅱ)因为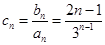 ,所以
,所以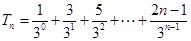 .
.
则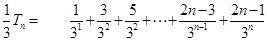 , 7分
, 7分
两式相减得: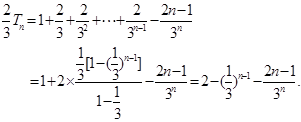 8分
8分
所以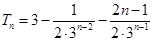
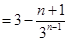 . 9分
. 9分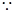
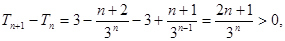
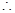
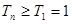 . 若
. 若 恒成立,则
恒成立,则
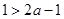 ,
,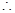
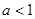 . 12分
. 12分
考点:数列的通项公式和求和
点评:该试题是常规试题,也是高考中的重点知识,需要熟练的掌握,属于基础题。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
等比数列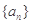 的前
的前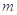 项和为4,前
项和为4,前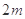 项和为12,则它的前
项和为12,则它的前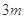 项和是
项和是
| A.28 | B.48 | C.36 | D.52 |
 ,求n的值;
,求n的值; }是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为
}是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为
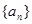 中,
中,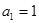 ,且
,且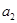 是
是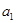 和
和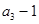 的等差中项.
的等差中项.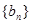 满足
满足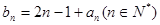 ,求
,求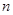 项和
项和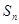 .
.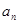 }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;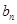 }满足:
}满足: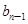 =
=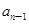 (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.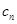 =
=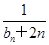 (n∈N﹡),若{
(n∈N﹡),若{ ,求
,求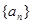 是公差不为零的等差数列,
是公差不为零的等差数列, 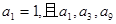 成等比数列.
成等比数列.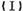 求数列
求数列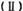 求数列
求数列 的前n项和
的前n项和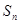
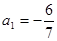 ,
, (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),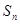 为数列{an}的前
为数列{an}的前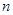 项和.
项和.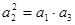 ,求
,求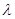 的值;
的值;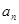 ;
;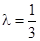 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.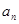 }的前n 项和为
}的前n 项和为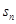 ,已知
,已知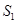 ,
,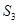 ,
,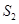 成等差数列
成等差数列 -
-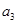 =3,求
=3,求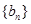 满足
满足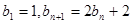 ,
,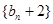 为等比数列 (2)求数列
为等比数列 (2)求数列