题目内容
设函数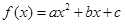 中,
中,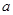 为奇数,
为奇数,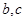 均为整数,且
均为整数,且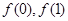 均为奇数.求证:
均为奇数.求证: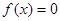 无整数根。
无整数根。
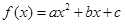 中,
中,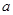 为奇数,
为奇数,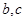 均为整数,且
均为整数,且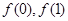 均为奇数.求证:
均为奇数.求证: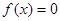 无整数根。
无整数根。详见解析.
试题分析:采用反证法,假设
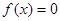 有整数根
有整数根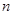 ,则
,则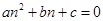 ,进而
,进而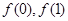 均为奇数,即
均为奇数,即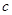 为奇数,
为奇数,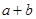 为偶数,即可得到
为偶数,即可得到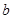 也为奇数,即可得到
也为奇数,即可得到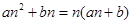 为奇数,即
为奇数,即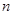 与
与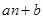 均为奇数,这与
均为奇数,这与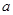 ,
,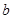 为奇数,
为奇数,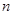 为奇数时,
为奇数时,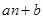 为偶数矛盾,故命题得证.
为偶数矛盾,故命题得证.证明:假设
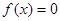 有整数根
有整数根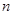 ,则
,则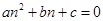 (2分)
(2分) 而
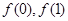 均为奇数,即
均为奇数,即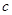 为奇数,
为奇数,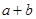 为偶数,(4分),
为偶数,(4分),∵
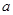 为奇数,∴
为奇数,∴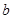 也为奇数 (6分)
也为奇数 (6分)∵
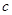 为奇数,∴
为奇数,∴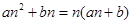 为奇数;∴
为奇数;∴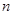 与
与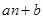 均为奇数 (9分)
均为奇数 (9分)∵
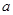 ,
,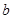 为奇数,
为奇数,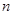 为奇数,∴
为奇数,∴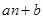 又为偶数 矛盾 (11分)
又为偶数 矛盾 (11分)∴
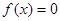 无整数根 (12分)
无整数根 (12分)
练习册系列答案
相关题目
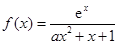 ,其中
,其中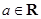 .
.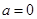 ,求函数
,求函数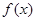 的定义域和极值;
的定义域和极值;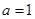 时,试确定函数
时,试确定函数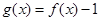 的零点个数,并证明.
的零点个数,并证明.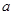 和
和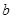 ,定义运算“
,定义运算“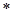 ”:
”: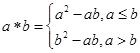 ,设
,设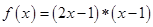 ,且关于
,且关于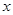 的方程为
的方程为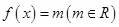 恰有三个互不相等的实数根
恰有三个互不相等的实数根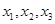 ,则
,则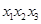 的取值范围是___________.
的取值范围是___________.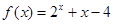 ,则函数
,则函数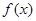 的零点位于区间( )
的零点位于区间( )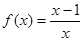 ,则方程
,则方程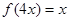 的根是( )
的根是( )