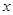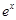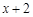题目内容
已知函数f(x)＝ax3－3ax＋3a－5至少有两个零点，则实数a的取值范围是（ ）
| A．[1,4] | B．[2,5] | C．[1,5] | D．[-5,-1] |
C
∵f′(x)＝3ax2－3a=3a(x2-1)=3a(x-1)(x+1)
若a＝0，则f(x)＝－5与题意不符，∴a≠0，
令f′(x)＝0,则x=1或x=-1,即f(x)在x=1或x=-1处取得极大或极小值
∴由题意知f(－1)·f(1)＝5(a－1)(a－5)≤0，∴1≤a≤5．
若a＝0，则f(x)＝－5与题意不符，∴a≠0，
令f′(x)＝0,则x=1或x=-1,即f(x)在x=1或x=-1处取得极大或极小值
∴由题意知f(－1)·f(1)＝5(a－1)(a－5)≤0，∴1≤a≤5．
练习册系列答案
相关题目
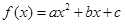中，
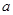为奇数，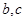
均为整数，且
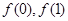均为奇数.求证：
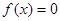无整数根。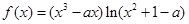
（
）
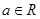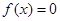有3个不同的根，求实数
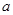的取值范围；
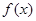在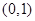
上恰有两个极值点
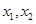，且满足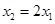
，若存在，求实数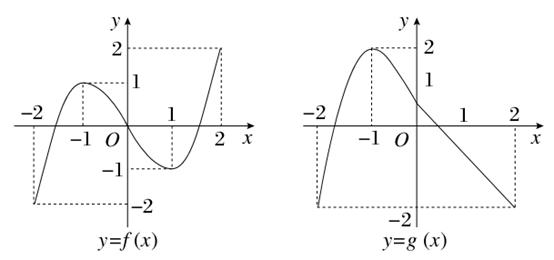
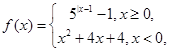若关于x的方程
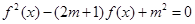有7个不同的实数解，则m=( ).
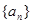和等比数列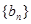
的首项均为1，且公差
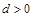，公比
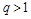，则集合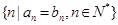
的元素个数最多有 个．
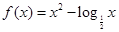的零点个数为（ ）
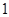
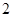
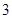
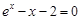的一个零点所在的区间是
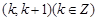，则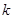
的值为（ ）
