题目内容
如图,已知圆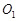 与圆
与圆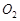 外切于点
外切于点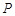 ,直线
,直线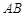 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于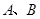 两点,
两点,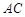 是圆
是圆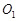 的直径,过
的直径,过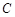 作圆
作圆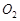 的切线,切点为
的切线,切点为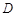 .
.
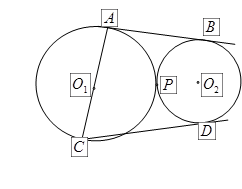
(Ⅰ)求证: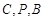 三点共线;
三点共线;
(Ⅱ)求证: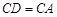 .
.
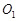 与圆
与圆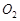 外切于点
外切于点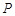 ,直线
,直线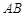 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于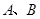 两点,
两点,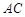 是圆
是圆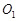 的直径,过
的直径,过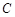 作圆
作圆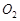 的切线,切点为
的切线,切点为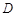 .
.
(Ⅰ)求证:
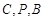 三点共线;
三点共线;(Ⅱ)求证:
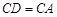 .
.证明见解析
试题分析:(I)连接
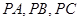 ,由于
,由于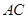 是圆
是圆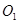 的直径,可得
的直径,可得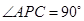 .作圆
.作圆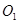 与圆
与圆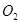 的内公切线
的内公切线 交
交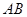 与点
与点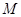 .利用切线的性质可得:
.利用切线的性质可得: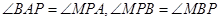 ,再利用三角形的内角和定理可得
,再利用三角形的内角和定理可得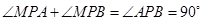 ,进而证明三点共线.
,进而证明三点共线.(II)由切线的性质可得
 ,利用射影定理可得
,利用射影定理可得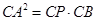 .再利用切割线定理可得
.再利用切割线定理可得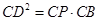 ,即可证明.
,即可证明.试题解析:(Ⅰ)连结PC,PA,PB,BO2,
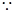
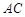 是圆O1的直径
是圆O1的直径 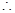
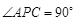 2分
2分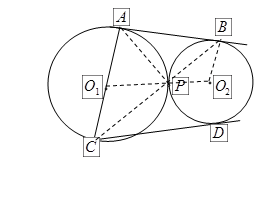
连结O1O2必过点P
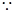
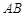 是两圆的外公切线,
是两圆的外公切线, 为切点
为切点
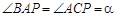
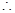
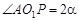
由于

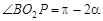
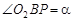
又因为
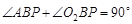
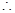
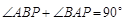
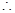
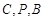 三点共线 5分
三点共线 5分(温馨提示:本题还可以利用作出内公切线等方法证明出结论,请判卷老师酌情给分!)
(Ⅱ)
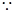 CD切圆O2于点D
CD切圆O2于点D 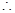
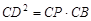 7分
7分在
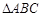 中,
中,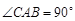 ,又
,又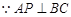
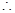
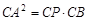
故
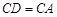 10分
10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
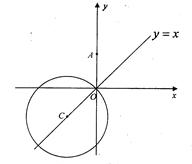
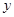 轴相切,圆心C在直线
轴相切,圆心C在直线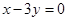 上,且被直线
上,且被直线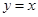 截得的弦长为
截得的弦长为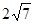 ,求圆C的方程.
,求圆C的方程.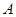 (-1,1),
(-1,1),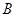 (1,3).
(1,3).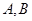 两点的直线方程;
两点的直线方程;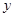 轴上的圆的方程.
轴上的圆的方程.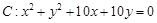 ,点
,点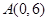 .
.
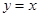 上,经过点
上,经过点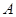 ,且与圆
,且与圆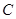 相外切的圆
相外切的圆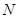 的方程;
的方程;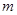 与圆
与圆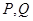 两点,且圆弧
两点,且圆弧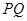 恰为圆
恰为圆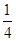 ,求直线
,求直线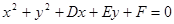 关于直线
关于直线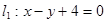 和直线
和直线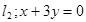 都对称,则
都对称,则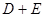 的值为( )
的值为( )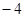
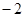
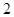
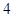
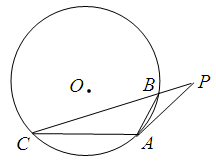
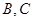 为圆
为圆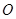 上的两个点,
上的两个点,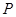 为
为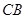 延长线上一点,
延长线上一点,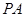 为圆
为圆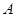 为切点. 若
为切点. 若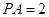 ,
,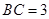 ,则
,则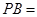 ______;
______;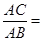 ______.
______.
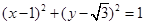 上的一个动点,A(
上的一个动点,A(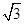 ,1),则
,1),则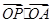 的最小值为______.
的最小值为______.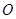 外一点
外一点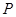 作圆的割线
作圆的割线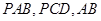 是圆
是圆 ,则
,则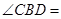 .
.