题目内容
已知数列{an}的通项公式an=log2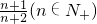 ,设其前n项和为Sn,则使Sn<-5成立的正整数n
,设其前n项和为Sn,则使Sn<-5成立的正整数n
- A.有最小值63
- B.有最大值63
- C.有最小值31
- D.有最大值31
A
分析:先有{an}的通项公式和对数的运算性质,求出Sn,再把Sn<-5转化为关于n的不等式即可.
解答:∵an=log2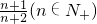 ,
,
∴Sn=a1+a2+a3+…+an=log2 +log2
+log2 +…+log2
+…+log2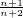 =log2
=log2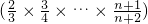 =log2
=log2 ,
,
又因为Sn<-5=log2 ?
?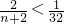 ?n>62,故使Sn<-5成立的正整数n有最小值:63
?n>62,故使Sn<-5成立的正整数n有最小值:63
故选 A
点评:本题考查了数列的求和以及对数的运算性质,是一道基础题.
分析:先有{an}的通项公式和对数的运算性质,求出Sn,再把Sn<-5转化为关于n的不等式即可.
解答:∵an=log2
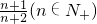 ,
,∴Sn=a1+a2+a3+…+an=log2
 +log2
+log2 +…+log2
+…+log2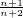 =log2
=log2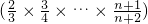 =log2
=log2 ,
,又因为Sn<-5=log2
 ?
?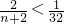 ?n>62,故使Sn<-5成立的正整数n有最小值:63
?n>62,故使Sn<-5成立的正整数n有最小值:63故选 A
点评:本题考查了数列的求和以及对数的运算性质,是一道基础题.

练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|