题目内容
若不等式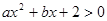
的解为
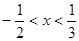，则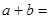
（ ）
| A．14 | B．-14 | C．-2 | D．12 |
B
解析试题分析：∵不等式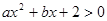的解为，∴
，∴
，∴
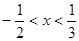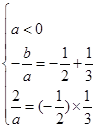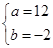，故选B
考点：本题考查了一元二次不等式的解法及韦达定理的运用
点评：掌握三个“二次”的关系是解决此类含参不等式的关键，属基础题
练习册系列答案
相关题目
若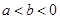
,则下列不等式:①
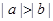;②
;③
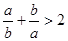;④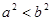
中,正确的有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
不等式│3-x│＜2的解集是 （ ）．
| A．{x│x＞5或x＜1} | B．{x│1＜x＜5} | C．{x│-5＜x＜-1} | D．{x│x＞1} |
不等式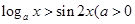
且
对任意
都成立，则
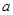的取值
范围为
A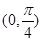． | B． | C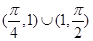． | D． |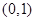
若不等式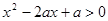
，对
恒成立,则关于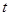
的不等式
的解集为 ( )
A． | B． |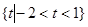
C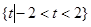． | D． |
方程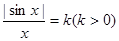
有且仅有两个不同的实数解
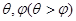，则以下结论正确的为( )
A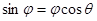． | B． |
C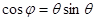． | D． |
不等式
对任意实数
恒成立，则实数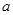
的取值范围为（ ）
A． | B． |
C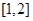． | D． |
若不等式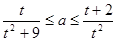
在
上恒成立,则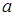
的取值范围是（ ）
A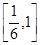． | B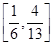． | C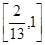． | D． |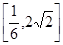
已知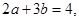
则
的最小值为（ ）
A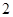． | B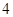． | C． | D． |