题目内容
不等式 对任意实数
对任意实数 恒成立,则实数
恒成立,则实数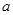 的取值范围为( )
的取值范围为( )
A. | B. |
C.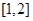 | D. |
A
解析试题分析:根据几何意义易知函数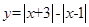 的最大值为4,所以要满足不等式
的最大值为4,所以要满足不等式 对任意实数
对任意实数 恒成立,只需
恒成立,只需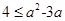 恒成立,所以
恒成立,所以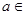
 。
。
考点:含绝对值不等式的解法;恒成立问题。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: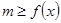 在
在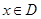 上恒成立
上恒成立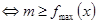 ;思路2:
;思路2: 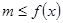 在
在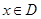 上恒成立
上恒成立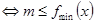 。
。

练习册系列答案
相关题目
不等式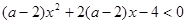 对于
对于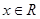 恒成立,则实数
恒成立,则实数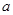 的取值范围为( )
的取值范围为( )
A.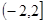 | B. | C.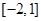 | D.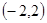 |
不等式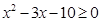 的解集是
的解集是
A.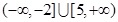 | B.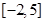 | C.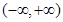 | D.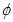 |
若不等式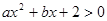 的解为
的解为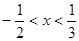 ,则
,则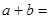 ( )
( )
| A.14 | B.-14 | C.-2 | D.12 |
不等式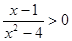 的解集是 ( )
的解集是 ( )
A.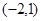 | B.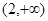 | C.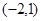  | D.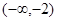 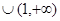 |
若不等式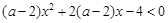 对一切
对一切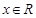 恒成立,则实数
恒成立,则实数 取值的集合( )
取值的集合( )
A.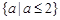 | B.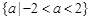 |
C.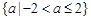 | D.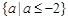 |
不等式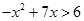 的解集是
的解集是
A.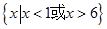 | B.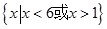 |
C.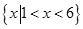 | D.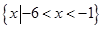 |
已知函数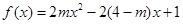 ,
,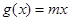 ,若对于任一实数
,若对于任一实数 ,
, 与
与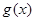 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数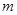 的取值范围是( )
的取值范围是( )
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
不等式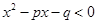 的解集是
的解集是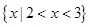 ,则不等式
,则不等式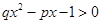 的解集是
的解集是
A.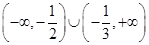 | B.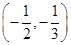 |
C.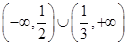 | D.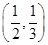 |