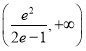题目内容
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①看两班的平均数易知正确;②看两班的中位数正确;③看两班的众数正确;④看两班的方差.
①从表看出甲、乙两班学生的平均成绩相同,正确;
②因为乙班的中位数比甲班的小,所以正确;
③根据甲、乙两班的众数,所以正确;
④因为乙班的方差比甲的大,所以波动比甲班大,所以错误
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
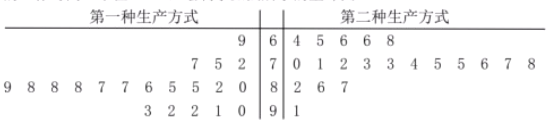
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表,再根据列联表,能否有99.9%的把握认为两种生产方式的效率有差异?
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
附: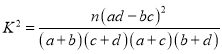 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |