题目内容
已知在△ABC中,内角A,B,C所对的边分别为a,b,c,且acos C+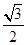 c=b.
c=b.
(1)求角A;
(2)若a=1,且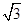 c-2b=1,求角B.
c-2b=1,求角B.
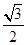 c=b.
c=b.(1)求角A;
(2)若a=1,且
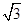 c-2b=1,求角B.
c-2b=1,求角B.(1) (2)
(2)
 (2)
(2)
解:(1)由acos C+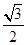 c=b,
c=b,
得sin Acos C+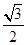 sin C=sin B,
sin C=sin B,
而sin B=sin(A+C)
=sin Acos C+cos Asin C,
则可得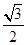 sin C=cos Asin C.
sin C=cos Asin C.
又sin C>0,则cos A=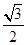 ,即A=
,即A= .
.
(2)由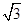 c-2b=1,得
c-2b=1,得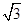 c-2b=a,
c-2b=a,
即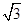 sin C-2sin B=sin A.
sin C-2sin B=sin A.
又∵A= ,∴C=
,∴C= -B,
-B,
∴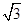 sin
sin -2sin B=
-2sin B= ,
,
整理得cos =
= .
.
∵0<B< ,∴
,∴ <B+
<B+ <π.
<π.
∴B+ =
= ,即B=
,即B= .
.
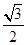 c=b,
c=b,得sin Acos C+
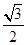 sin C=sin B,
sin C=sin B,而sin B=sin(A+C)
=sin Acos C+cos Asin C,
则可得
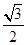 sin C=cos Asin C.
sin C=cos Asin C.又sin C>0,则cos A=
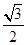 ,即A=
,即A= .
.(2)由
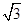 c-2b=1,得
c-2b=1,得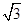 c-2b=a,
c-2b=a,即
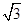 sin C-2sin B=sin A.
sin C-2sin B=sin A.又∵A=
 ,∴C=
,∴C= -B,
-B,∴
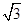 sin
sin -2sin B=
-2sin B= ,
,整理得cos
 =
= .
.∵0<B<
 ,∴
,∴ <B+
<B+ <π.
<π.∴B+
 =
= ,即B=
,即B= .
.
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 所对的边分别为
所对的边分别为 且
且 .
.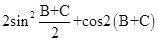 ;
;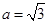 ,求
,求 面积的最大值.
面积的最大值. 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按
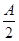 sin
sin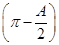 +sin2
+sin2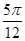 ,a=
,a=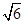 ,求b的值.
,求b的值. ,BC=2,C=60°,则边长AB的长度等于________.
,BC=2,C=60°,则边长AB的长度等于________. 中,已知
中,已知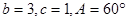 ,则
,则 = .
= . 中,若
中,若 则
则