题目内容
在 所对的边分别为
所对的边分别为 且
且 .
.
(1)求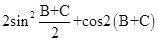 ;
;
(2)若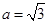 ,求
,求 面积的最大值.
面积的最大值.
 所对的边分别为
所对的边分别为 且
且 .
.(1)求
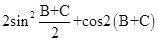 ;
;(2)若
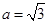 ,求
,求 面积的最大值.
面积的最大值.(1)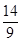 ;(2)
;(2)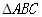 面积的最大值为
面积的最大值为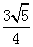 .
.
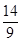 ;(2)
;(2)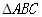 面积的最大值为
面积的最大值为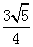 .
.试题分析:(1)求
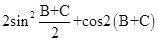 ,首先利用三角形内角和等于
,首先利用三角形内角和等于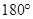 对其转化成单角,再利用倍角公式进行恒等变化得
对其转化成单角,再利用倍角公式进行恒等变化得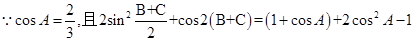 ,由已知
,由已知 ,带入即可;(2)若
,带入即可;(2)若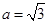 ,求
,求 面积的最大值,由已知
面积的最大值,由已知 ,可求出
,可求出 ,可利用
,可利用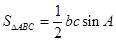 ,因此求
,因此求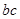 即可,又因为
即可,又因为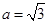 ,可想到利用余弦定理来解,由余弦定理得,
,可想到利用余弦定理来解,由余弦定理得,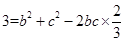 ,利用基本不等式可求出
,利用基本不等式可求出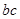 的最大值,从而得
的最大值,从而得 面积的最大值.
面积的最大值.试题解析:(1)
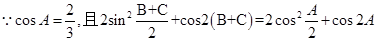
 6分
6分(2)
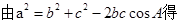
即
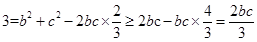 ,
,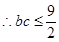 ,
,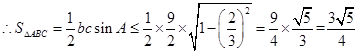
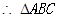 面积的最大值为
面积的最大值为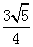 12分
12分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 中,已知
中,已知 ,
, 是
是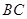 边上的一点,
边上的一点,

 的值;
的值; 的值。
的值。 。
。 ,求
,求 的值。
的值。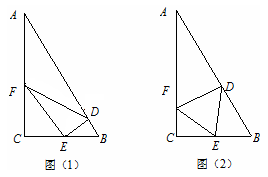
 ,且C=120°.
,且C=120°. 中,若
中,若 ,则
,则


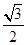 c=b.
c=b.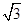 c-2b=1,求角B.
c-2b=1,求角B. 中,
中,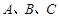 所对边分别为
所对边分别为 、
、 、
、 .若
.若 ,则
,则 .
. 中,
中, ,
, ,
, ,则
,则 .
.