题目内容
已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为________.
15

由于三边长构成公差为4的等差数列,故可设三边长分别为x-4,x,x+4.
由一个内角为120°知其必是最长边x+4所对的角.
由余弦定理,得(x+4)2=x2+(x-4)2-2x(x-4)·cos 120°,∴2x2-20x=0,
∴x=0(舍去)或x=10.
∴S△ABC=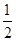 ×(10-4)×10×sin 120°=15
×(10-4)×10×sin 120°=15 .
.
由一个内角为120°知其必是最长边x+4所对的角.
由余弦定理,得(x+4)2=x2+(x-4)2-2x(x-4)·cos 120°,∴2x2-20x=0,
∴x=0(舍去)或x=10.
∴S△ABC=
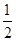 ×(10-4)×10×sin 120°=15
×(10-4)×10×sin 120°=15 .
.
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
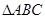 中,
中,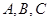 的对边分别为
的对边分别为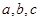 且
且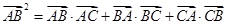 .
.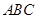 的形状,并求
的形状,并求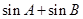 的取值范围;
的取值范围;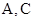 分别在
分别在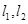 上运动,
上运动,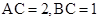 ,若直线
,若直线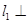 直线
直线 ,且相交于点
,且相交于点 ,求
,求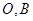 间距离的取值范围.
间距离的取值范围.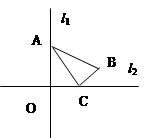
 .
. 的最小正周期;
的最小正周期;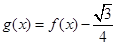 ,求
,求 在区间
在区间 上的值域.
上的值域. 。
。 ,求
,求 的值。
的值。 中,角A、B,C,所对的边分别为
中,角A、B,C,所对的边分别为 ,且
,且
 的值;
的值; ,求
,求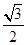 c=b.
c=b.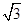 c-2b=1,求角B.
c-2b=1,求角B. 中,
中,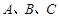 所对边分别为
所对边分别为 、
、 、
、 .若
.若 ,则
,则 .
. 中,
中, ,
, ,
, ,则
,则 .
. ,则cos2
,则cos2 =( )
=( )

