Question

如图，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=

2

2

AD，若E、F分别为线段PC、BD的中点．
（1）求证：直线EF∥平面PAD；
（2）求证：平面PDC⊥平面PAD；
（3）线段AB上是否存在一点M，使二面角M-PD-C为45°．

Answer 1

分析：取AD的中点O，连接OP，OF．因为PA=PD，所以PO⊥AD，再根据侧面PAD⊥底面ABCD，结合平面与平面垂直的性质定理，得到PO⊥平面ABCD，然后在△PAD中利用勾股定理的逆定理得到△PAD是等腰直角三角形，并且OP=OA=OD=

a

2

．这样就可以O为原点，直线OA、OF、OP为x、y、z轴建立空间直线坐标系，得到A、B、C、D、F、P各点的坐标．
（1）分别算出向量

EF

和平面PAD的法向量

OF

的坐标，可以算出它们的数量积为零，从而得到

OF

和

EF

互相垂直，证出直线EF∥平面PAD；
（2）取平面PAD内的向量

PA

，通过坐标计算证出向量

PA

与

CD

互相垂直，从而直线PA、CD互相垂直，再结合PA、PD互相垂直，根据线面垂直的判定定理得到PA⊥平面PDC，结合面面垂直的判定定理证出平面PDC⊥平面PAD；
（3）先假设线段AB上存在一点M（

a

2

，m，0），满足二面角M-PD-C大小为45°，然后再设平面PBD的法向量为

n

=（x，y，z），结合向量

n

与

DP

、

n

与

DM

的数量积都等于0，联列方程组解出x，y，z的比例，取x=1，得到向量

n

=（1，-

a

m

，-1），最后根据两个向量

n

与平面PDC的法向量为

PA

=（

a

2

，0，-

a

2

）的夹角为45°，用数量积公式解出AM=

2

2

a，从而找到符合题意的M点．

解答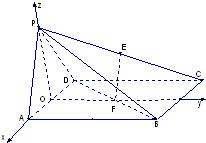：解：如图，取AD的中点O，连接OP，OF．
∵PA=PD，∴PO⊥AD．
∵侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD
∴PO⊥底面ABCD，
∵O、F分别为AD、BD的中点，
∴OF∥AB，结合ABCD是正方形，
可得OF⊥AD．
∵PA=PD=

2

2

AD，
∴PA⊥PD，OP=OA=OD=

a

2

．
以O为原点，直线OA、OF、OP为x、y、z轴建立空间直线坐标系，
则有A（

a

2

，0，0），F（0，

a

2

，0），D（-

a

2

，0，0），P（0，0，

a

2

），B（

a

2

，a，0），C（-

a

2

，a，0），．
∵E为PC的中点，∴E（-

a

4

，

a

2

，

a

4

）．
（1）由OF⊥平面PAD，得平面PAD的法向量为

OF

=（0，

a

2

，0），
而

EF

=（

a

4

，0，-

a

4

），且

OF

•

EF

=0×

a

4

+

a

2

×0+0×(-

a

4

)=0，
∴EF∥平面 PAD
（2）

PA

=（

a

2

，0，-

a

2

），

CD

=（0，a，0）
∴

PA

•

CD

=

a

2

×0+0×a+( -

a

2

)×0=0，
∴

PA

⊥

CD

，从而PA⊥CD，
又∵PA⊥PD，PD∩CD=D，
∴PA⊥平面PDC，而PA?PAD，
∴平面PDC⊥平面PAD
（3）由（2）知平面PDC的法向量为

PA

=（

a

2

，0，-

a

2

）．
设线段AB上存在一点M（

a

2

，m，0），使二面角M-PD-C为45°．
再设平面PBD的法向量为

n

=（x，y，z）．
∵

DP

=(

a

2

，0，

a

2

)，

DM

=(a，m，0)，
∴由

n

•

DP

=0，

n

•

DM

=0，可得

a 2 x+ a 2 z=0 ax+my=0

，
令x=1，则

n

=(1，-

a

m

，-1)，二面角M-PD-C为45°
∴cos＜

n

，

PA

＞=

n • PA

| n |•| PA |

=

a

2+ a2 m2 • 2 a 2

=

2

2

．
∴m=

2

2

a
即线段AB上存在一点M，当AM=

2

2

a时，二面角M-PD-C的大小为45°．

点评：本题以一个特殊四棱锥为例，考查了平面与平面垂直的判定、直线与平面平行的判定和用空间向量求平面间的夹角和与二面角有关的立体几何综问题等知识点，属于中档题．