题目内容
【题目】已知椭圆M: ![]() +
+ ![]() =1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B,经过点F的直线l与椭圆M交于C,D两点.
=1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B,经过点F的直线l与椭圆M交于C,D两点.
(Ⅰ)求椭圆方程;
(Ⅱ)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
【答案】解:(Ⅰ)因为F(﹣1,0)为椭圆的焦点,所以c=1,
又b= ![]() ,所以a=2,
,所以a=2,
所以椭圆方程为 ![]() =1;
=1;
(Ⅱ)直线l无斜率时,直线方程为x=﹣1,
此时D(﹣1, ![]() ),C(﹣1,﹣
),C(﹣1,﹣ ![]() ),△ABD,△ABC面积相等,|S1﹣S2|=0,
),△ABD,△ABC面积相等,|S1﹣S2|=0,
当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),
设C(x1,y1),D(x2,y2),
和椭圆方程联立,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
显然△>0,方程有根,且x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
此时|S1﹣S2|=2||y1|﹣|y2||=2|y1+y2|=2|k(x2+1)+k(x1+1)|
=2|k(x2+x1)+2k|= ![]() =
= 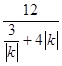 ≤
≤ ![]() =
= ![]() ,(k=±
,(k=± ![]() 时等号成立)
时等号成立)
所以|S1﹣S2|的最大值为 ![]()
【解析】(Ⅰ)由焦点F坐标可求c值,根据a,b,c的平方关系可求得a值;(Ⅱ)当直线l不存在斜率时可得,|S1﹣S2|=0;当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),与椭圆方程联立消y可得x的方程,根据韦达定理可用k表示x1+x2,x1x2,|S1﹣S2|可转化为关于x1,x2的式子,进而变为关于k的表达式,再用基本不等式即可求得其最大值.

练习册系列答案
相关题目