题目内容
2.已知圆的圆心为坐标原点,且经过点(-1,$\sqrt{3}$).(1)求圆的方程;
(2)若直线l1:x-$\sqrt{3}$y+b=0与此圆有且只有一个公共点,求b的值;
(3)求直线l2:x-$\sqrt{3}y+2\sqrt{3}$=0被此圆截得的弦长.
分析 (1)由已知得圆心为(0,0),由两点间距离公式求出半径,由此能求出圆的方程.
(2)由已知得l1与圆相切,由圆心(0,0)到l1的距离等于半径2,利用点到直线的距离公式能求出b.
(3)先求出圆心(0,0)到l2的距离d,所截弦长l=2$\sqrt{{r}^{2}-{d}^{2}}$,由此能求出弦长.
解答 解:(1)∵圆的圆心为坐标原点,且经过点(-1,$\sqrt{3}$),
∴圆心为(0,0),半径r=$\sqrt{(0+1)^{2}+(0-\sqrt{3})^{2}}$=2,
∴圆的方程为x2+y2=4.…(4分)
(2)∵直线l1:x-$\sqrt{3}$y+b=0与此圆有且只有一个公共点,
∴l1与圆相切,则圆心(0,0)到l1的距离等于半径2,即$\frac{|b|}{\sqrt{1+3}}$=2,
解得b=±4.…(8分)
(3)∵直线l2:x-$\sqrt{3}y+2\sqrt{3}$=0与圆x2+y2=4相交,
圆心(0,0)到l2的距离d=$\frac{|2\sqrt{3}|}{2}$=$\sqrt{3}$,
∴所截弦长l=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{4-3}$=2.…(14分)
点评 本题考查圆的方程的求法,考查实数值的求法,考查弦长的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
13.已知实数x、y、z满足x2+y2+z2=4,则(2x-y)2+(2y-z)2+(2z-x)2的最大值是( )
| A. | 12 | B. | 20 | C. | 28 | D. | 36 |
17.P是边长为a的正三角ABC所在平面外一点,PA=PB=PC=a,E、F是AB和PC的中点,则异面直线PA与EF所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.关于x的不等式$\frac{2x-3a}{x+2a}≤1(a<0)$的解集是( )
| A. | [5a,-2a) | B. | (-∞,5a]∪(-2a,+∞) | C. | (-2a,5a]? | D. | (-∞,5a] |
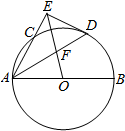 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.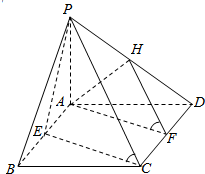 如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.
如图所示,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2CD=2,E,F,H分别为AB,CD,PD的中点,求证:(1)平面AFH∥平面PCE;(2)求VD-AHF.