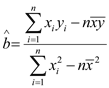题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 且与
且与![]() 轴不重合的直线
轴不重合的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(ⅰ)求![]() 的方程;
的方程;
(ⅱ)记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)
;(ⅱ)![]() .
.
【解析】
(1)根据椭圆的定义,根据条件列出方程求解即可;
(2)(ⅰ)设M,N坐标分边为![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,结合椭圆方程可得BM、BN方程,并得出点P、Q坐标的表达式,根据圆过点
,结合椭圆方程可得BM、BN方程,并得出点P、Q坐标的表达式,根据圆过点![]() ,故向量
,故向量![]() ,列方程可得m的值;(ⅱ)由(ⅰ),将
,列方程可得m的值;(ⅱ)由(ⅰ),将![]() ,
,![]() 的面积
的面积![]() ,
,![]() 转换为
转换为![]() 、
、![]() 的表达式,相比可得出
的表达式,相比可得出![]() 的取值范围.
的取值范围.
解:(1)依题意得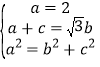 ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)(ⅰ)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
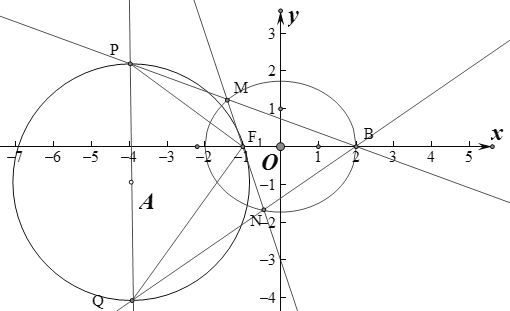
由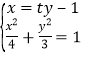 得
得![]() ,
,
显然![]() ,且
,且![]() ,
,![]() ,
,
直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
∵以![]() 为直径的圆过点
为直径的圆过点![]() ,∴
,∴![]() ,
,
∴![]()
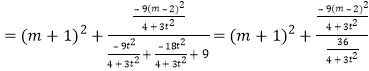
![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
∴![]() 的方程为
的方程为![]() .
.
(ⅱ)由(ⅰ),![]()
![]()
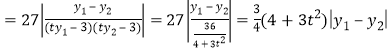 ,
,
∴![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”
之间为“体质不合格”![]() 现从两个年级中各随机抽取8名学生,测试成绩如下:
现从两个年级中各随机抽取8名学生,测试成绩如下:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a,b是正整数.
(1)若该校高一年级有200名学生,试估计高一年级“体质优秀”的学生人数;
(2)从高一年级抽取的学生中再随机选取3人,求这3人中,恰有1人“体质良好”的概率;
(3)设两个年级被抽取学生的测试成绩的平均数相等,当高二年被抽取学生的测试成绩的方差最小时,写出a,b的值![]() 结论不要求证明
结论不要求证明![]()