题目内容
【题目】设圆![]() 的圆心为A,直线
的圆心为A,直线![]() 过点B(1,0)且与
过点B(1,0)且与![]() 轴不重合,
轴不重合,![]() 交圆A于C,D两点,过B作AC的平行线交AD于点E.
交圆A于C,D两点,过B作AC的平行线交AD于点E.
(Ⅰ)证明:![]() 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(Ⅱ)设点E的轨迹为曲线C1,直线![]() 交C1于M,N两点,过B且与
交C1于M,N两点,过B且与![]() 垂直的直线与C1交于P,Q两点, 求证:
垂直的直线与C1交于P,Q两点, 求证:![]() 是定值,并求出该定值.
是定值,并求出该定值.
【答案】(I)![]() (
(![]() );(II)
);(II)![]()
【解析】
(I)根据几何关系,即可证明![]() 为定值,再利用椭圆的定义即可求出点E的轨迹方程;
为定值,再利用椭圆的定义即可求出点E的轨迹方程;
(Ⅱ)利用点斜式设出直线![]() 的方程,与椭圆方程联立方程组,得到关于
的方程,与椭圆方程联立方程组,得到关于![]() 的一元二次方程,利用根与系数关系以及弦长公式表示出
的一元二次方程,利用根与系数关系以及弦长公式表示出![]() ,同理可得
,同理可得![]() ,代入
,代入![]() 中进行化简即可证明
中进行化简即可证明![]() 为定值。
为定值。
(I)因为![]() ,
,![]() ,故
,故![]() ,
,
所以![]() ,故
,故![]() .
.
又圆![]() 的标准方程为
的标准方程为![]() ,从而
,从而![]() ,
,
所以![]() ,由题设得
,由题设得![]() ,
,![]() ,
,![]() ,
,
由椭圆定义可得点![]() 的轨迹方程为:
的轨迹方程为:![]() (
(![]() ).
).
(II)依题意:![]() 与
与![]() 轴不垂直,设
轴不垂直,设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
由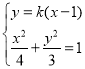 得,
得,![]() .
.
则![]() ,
,![]() .
.
所以![]() .
.
同理:![]() 故
故![]() (定值)
(定值)

练习册系列答案
相关题目