题目内容
【题目】在平面直角坐标系xOy中，直线l的参数方程为 
；在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为
(1)若a＝1，求C与l交点的直角坐标；
(2)若C上的点到l的距离的最大值为
，求a.
【答案】（1）
（2）
.
【解析】分析：（1）曲线
的极坐标方程化简后，利用
即可得曲线的直角坐标方程，将直线的参数方程化为普通方程，联立解方程即可的结果；（2）设上的点
，由点到直线距离公式、利用辅助角公式，根据三角函数的有界性列方程求解，从而可得结果.
详解：(1)曲线C的普通方程为 
当a=1时，直线l的普通方程为x＋y－2＝0.
由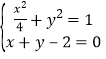 
解得
或
从而C与l的交点坐标是
.
(2)直线l的普通方程是x＋y－1－a＝0，故C上的点(2cos θ，sin θ)到l的距离为
当a≥－1时，d的最大值为
.
由题设得
，所以
当a<－1时，d的最大值为. 
由题设得，
所以
.
综上，
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】小明同学在寒假社会实践活动中，对白天平均气温与某家奶茶店的
品牌饮料销量之间的关系进行了分析研究，他分别记录了1月11日至1月15日的白天气温
（
）与该奶茶店的品牌饮料销量
（杯），得到如表数据：
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
（1）若先从这五组数据中抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；
（2）请根据所给五组数据，求出关于的线性回归方程式
；
（3）根据（2）所得的线性回归方程，若天气预报1月16号的白天平均气温为
，请预测该奶茶店这种饮料的销量.
（参考公式：
，
）
