题目内容
(本小题满分14分) 已知函数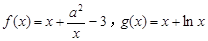 ,其中
,其中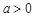 。
。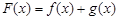 。
。
(1)若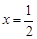 是函数
是函数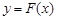 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若函数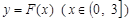 的图象上任意一点处切线的斜率
的图象上任意一点处切线的斜率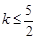 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数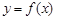 在
在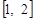 上有两个零点,求实数a的取值范围。
上有两个零点,求实数a的取值范围。
【答案】
(1)1(2)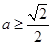 (3)
(3)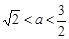
【解析】
试题分析:由题意知,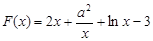 ,所以
,所以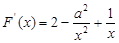 , ……2分
, ……2分
(1)所以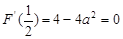 且
且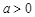 ,
,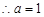 . ……4分
. ……4分
(2)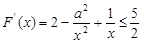 对任意的
对任意的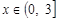 恒成立, ……5分
恒成立, ……5分
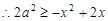 对任意的
对任意的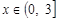 恒成立,
恒成立,
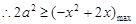 ,
,
而当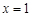 时,
时,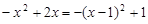 取最大值为1,
取最大值为1,
 ,且
,且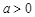 ,
,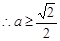 . ……7分
. ……7分
(3)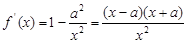 ,且
,且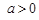 ,
,
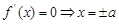 ;
;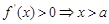 或
或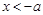 ;
;
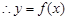 在
在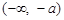 和
和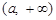 上递增;而在
上递增;而在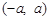 上递减。 ……8分
上递减。 ……8分
当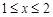 时
时
i)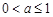 ,则
,则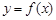 在
在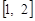 上递增,
上递增,
所以 在
在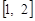 上不可能有两个零点。 ……9分
上不可能有两个零点。 ……9分
ii)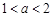 ,则
,则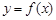 在
在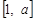 上递减,而在
上递减,而在 上递增。
上递增。
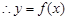 在
在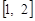 上有极小值(也就是最小值)
上有极小值(也就是最小值)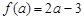 ,
,
而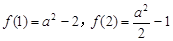 ,
,
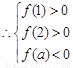
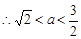 ,
,
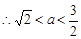 时,
时, 在
在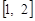 上有两个零点。 ……12分
上有两个零点。 ……12分
iii)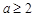 ,则
,则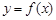 在
在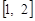 上递减,
上递减,
所以 在
在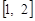 上不可能有两个零点。 ……13分
上不可能有两个零点。 ……13分
综上所述: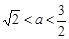 . ……14分
. ……14分
考点:本小题主要考查导数几何意义的应用、利用导数研究单调性和构造函数证明不等式以及基本不等式的应用,考查学生分析问题、解决问题的能力和构造能力以及运算求解能力.
点评:导数是研究函数的性质(尤其是单调性、极值、最值等)的有力工具,要灵活应用.

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)