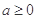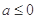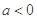题目内容
定义在R上的函数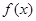
满足：
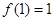，且对于任意的
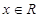,都有
＜
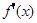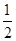，则不等式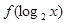
＞
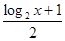的解集为 .
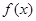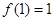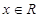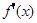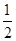满足：，且对于任意的,都有＜，则不等式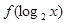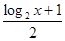＞的解集为 .(0,2)
试题分析：设g（x）=f（x）-
x，∵f′（x）＜,∴g′（x）=f′（x）-＜0，∴g（x）为减函数，又f（1）=1，∴f（log2x）＞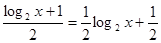
,即g（log2x）=f（log2x）-log2x＞=g（1）=f（1）-=g（log22），∴log2x＜log22，又y=log2x为底数是2的增函数，∴0＜x＜2，则不等式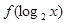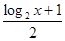＞的解集为（0，2）.
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
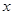元/本（9≤
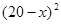万本．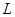
（万元）与每本书的定价
．
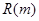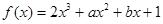的导数为
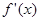,若函数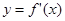
的图象关于直线
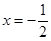对称，且函数
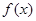在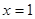
处取得极值.
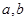的值；
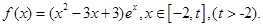
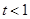时，求函数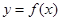
的单调区间;
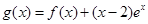，试问函数
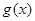在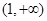
上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由.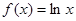
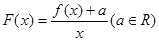，求
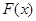的极大值；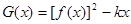
在定义域内单调递减，求满足此条件的实数k的取值范围.
x2－ln x的单调递减区间为 ( )． 
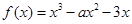在区间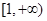
上是增函数，则实数
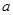的取值范围是 ．
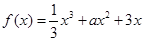在（0， 1）上不是单调函数，则实数
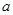的取值范围为 _____.
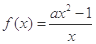在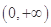
上单调递增，那么实数
的取值范围是（ ）
