题目内容
4.设f(x)是定义在N*上的函数,若f(1)=1,且对任意的x,y都有:f(x)+f(y)=f(x+y)-xy,求f(x)分析 利用赋值法,令y=1得f(x+1)-f(x)=x+1,然后利用累加法进行求解即可.
解答 解:以y=1代入,得:f(x)+f(1)=f(x+1)-x.
即f(x)+1=f(x+1)-x,
f(x+1)-f(x)=x+1,
则f(x)-f(x-1)=x,
f(x-1)-f(x-2)=x-1,
f(x-2)-f(x-3)=x-2,
…
f(2)-f(1)=2,
上面所有式子相加,
得:f(x)-f(1)=[(x)+(x-1)+(x-2)+(x-3)+…+3+2],
即f(x)=1+2+3+…+(x-1)+x=$\frac{x(1+x)}{2}$.
点评 本题主要考查函数解析式的求解,利用赋值法以及累加法是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.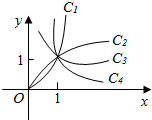 已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
 已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )| A. | -2,-$\frac{1}{2}$,$\frac{1}{2}$,2 | B. | 2,$\frac{1}{2}$,-$\frac{1}{2}$,-2 | C. | -$\frac{1}{2}$,-2,2,$\frac{1}{2}$ | D. | 2,$\frac{1}{2}$,-2,-$\frac{1}{2}$ |
9.直角三角形三边或成等差数列,且它的面积为18,那么周长为( )
| A. | 6$\sqrt{6}$ | B. | 12$\sqrt{3}$ | C. | 36$\sqrt{3}$ | D. | 9$\sqrt{3}$ |