题目内容
5.已知函数f(x)=|x-a|,(a∈R).(1)若当0≤x≤4时,f(x)≤2恒成立,求实数a的取值;
(2)当0≤a≤3时,求证:f(x+a)+f(x-a)≥f(ax)-af(x)
分析 (1)解|x-a|≤2得,a-2≤x≤a+2,由当0≤x≤4时,f(x)≤2恒成立,可得:$\left\{\begin{array}{l}a-2≤0\\ a+2≥4\end{array}\right.$,解得答案.
(2)由0≤a≤3可得|a-1|≤2,进而f(ax)-af(x)≤2a,f(x+a)+f(x-a)≥2a.进而得到答案.
解答 解:(1)解|x-a|≤2得,a-2≤x≤a+2,
∵当0≤x≤4时,f(x)≤2恒成立,
∴$\left\{\begin{array}{l}a-2≤0\\ a+2≥4\end{array}\right.$,
解得:a=2,
(2)∵0≤a≤3,
∴-1≤a-1≤2,
∴|a-1|≤2,
∴f(ax)-af(x)=|ax-a|-a|x-a|=|ax-a|-|ax-a2|≤|(ax-a)-(ax-a2)=|a2-a|=a|a-1|≤2a,
∵f(x+a)+f(x-a)=|x-2a|+|x|≥||(x-2a)-x|=|2a|=2a.
∴f(x+a)+f(x-a)≥f(ax)-af(x)
点评 本题主要考查绝对值不等式的解法,体现了等价转化以及分类讨论的数学思想,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15.已知直线x+y-k=0(k>0)与圆x2+y2=4交于不同的两点A、B,O是坐标原点,若$|{\overrightarrow{OA}+\overrightarrow{OB}}|=\frac{{\sqrt{3}}}{3}|{\overrightarrow{AB}}|$,则实数k=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
10.已知a为如图所示的算法框图中输出的结果,则a的值为( )


| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | -2 |
17.执行如图所示的程序框图,则输出的T值为( )
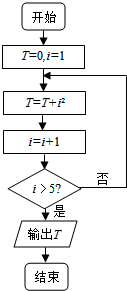

| A. | 30 | B. | 54 | C. | 55 | D. | 91 |
