题目内容
20.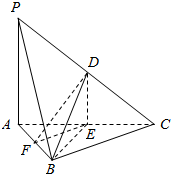 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:
(1)直线PA∥平面DEF;
(2)PA⊥AB.
分析 (1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF;
(2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可,再由DE∥PA,能证明PA⊥AB.
解答 证明:(1)证明:∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA?平面DEF,DE?平面DEF,
∴PA∥平面DEF.
(2)∵D、E为PC、AC的中点,∴DE=$\frac{1}{2}$PA=3,
又∵E、F为AC、AB的中点,∴EF=$\frac{1}{2}$BC=4,
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF,
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC,
∵DE∥PA,∴PA⊥平面ABC,
∵AB?平面ABC,∴PA⊥AB.
点评 本题考查了空间中的平行与垂直问题,解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系,是中档题.

练习册系列答案
相关题目
11.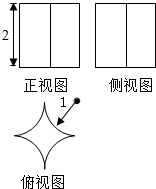 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )
 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )| A. | 8-π | B. | 8+π | C. | 8-2π | D. | 8+2π |
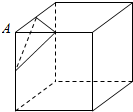 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论: