题目内容
已知函数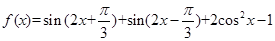 ,
, .
. 求函数
求函数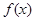 的最小正周期;
的最小正周期; 若函数
若函数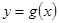 的图像和
的图像和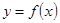 的图像关于直线
的图像关于直线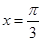 对称,求
对称,求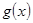 在
在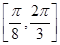 上的最大值和最小值.
上的最大值和最小值.
(1) .(2)
.(2)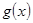 的最大值和最小值分别为
的最大值和最小值分别为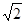 和
和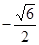 。
。
解析试题分析:(1)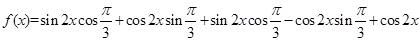
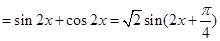
所以,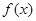 的最小正周期
的最小正周期 .
.
(2) 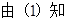
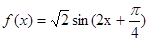
因为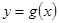 的图像和
的图像和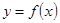 的图像关于直线
的图像关于直线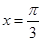 对称,且
对称,且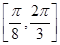 关于直线
关于直线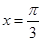 对称的区间为
对称的区间为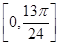 ,则
,则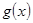 在
在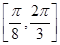 上的最大值和最小值即
上的最大值和最小值即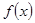 在
在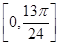 的最大值和最小值。
的最大值和最小值。
∵ ,∴
,∴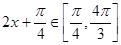 ,
,
∴当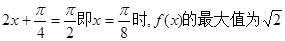 ;当
;当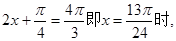
 。即
。即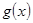 的最大值和最小值分别为
的最大值和最小值分别为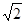 和
和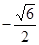 。
。
另法:因为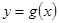 的图像和
的图像和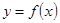 的图像关于直线
的图像关于直线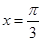 对称,故
对称,故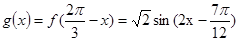
∵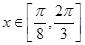 ,∴
,∴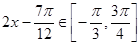 ,
,
当
当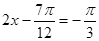 时
时 。
。
考点:和差倍半的三角函数公式,正弦型函数图象的变换,三角函数的图像和性质。
点评:典型题,本题综合性较强,利用三角公式,将研究对象“化一”,是高考要求的基本问题,在此基础上,进一步研究函数的图象和性质。(II)小题求指定范围内函数的最值,易于出错,应结合图象分析。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
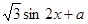 )(
)(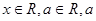 是常数),且
是常数),且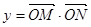 (O为坐标原点)
(O为坐标原点)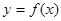 ;
;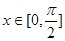 时,
时, 最大值为2013,求a的值.
最大值为2013,求a的值.
 化简成
化简成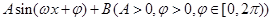 的形式;
的形式;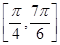 上的最大值和最小值.
上的最大值和最小值.
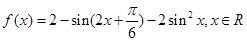 ,记
,记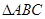 的内角
的内角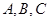 的对边长分别为
的对边长分别为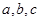 ,若
,若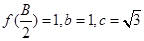 ,求
,求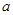 的值。
的值。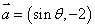 与
与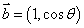 互相垂直,其中
互相垂直,其中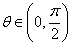 .
.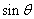 和
和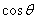 的值;
的值;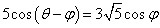 ,
,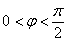 ,求
,求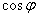 的值.
的值. .
.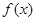 的最小正周期和单调增区间;
的最小正周期和单调增区间;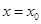 对称,且
对称,且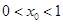 ,求
,求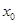 的值.
的值.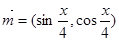 ,
,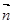 =(
=(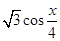 ,
, ),记
),记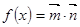 ;
;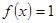 ,求
,求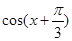 的值;
的值; 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.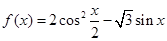 .
.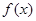 的最小正周期和值域;
的最小正周期和值域;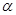 为第二象限角,且
为第二象限角,且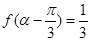 ,求
,求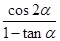 的值.
的值.