题目内容
(本小题满分14分)
设数列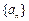 的前
的前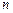 项和为
项和为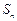 ,且
,且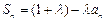
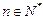 ,其中
,其中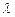 为常数,
为常数,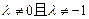 .
.
(1)求证:数列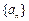 是等比数列;
是等比数列;
(2)若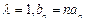 ,数列
,数列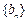 的前
的前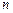 项和为
项和为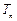 ,求证:当
,求证:当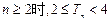 ;
;
(3)设数列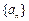 的公比为
的公比为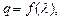 数列
数列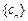 满足
满足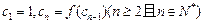 求证:
求证: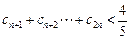 .
.
设数列
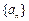 的前
的前 项和为
项和为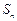 ,且
,且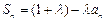
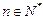 ,其中
,其中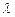 为常数,
为常数,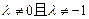 .
.(1)求证:数列
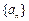 是等比数列;
是等比数列;(2)若
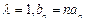 ,数列
,数列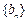 的前
的前 项和为
项和为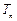 ,求证:当
,求证:当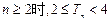 ;
;(3)设数列
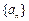 的公比为
的公比为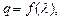 数列
数列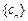 满足
满足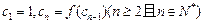 求证:
求证: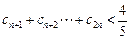 .
.略
解(1)由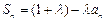 又
又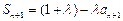 两式相减得
两式相减得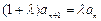
即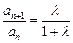 为常数,∴数列
为常数,∴数列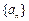 等比.
等比.
(2)由(1)知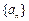 等比,又
等比,又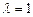 ,当
,当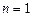 时,
时,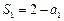 即
即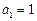
∴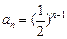 即
即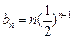
∴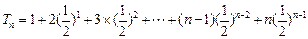
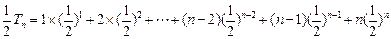
两式相减得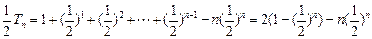
∴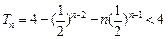 又
又 ∴
∴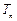 单调递增
单调递增
∴当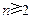 时,
时,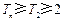 故当
故当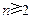 时
时 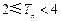
(3)由(1)知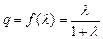 则
则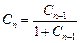 ∴
∴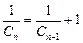
故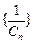 是首项
是首项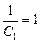 ,公差
,公差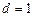 的等差数列. ∴
的等差数列. ∴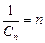 即
即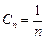
即证: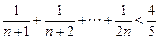
方法一:只须证 ,用数学归纳法证明(i)当
,用数学归纳法证明(i)当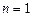 时,左
时,左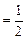 右边
右边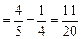 不等式成立,(ii)假设
不等式成立,(ii)假设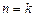 时不等式成立,
时不等式成立,
即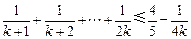 则当
则当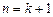 时
时
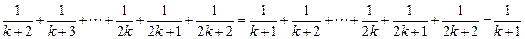
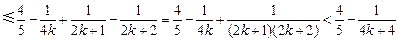
即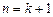 时也成立,综合(i)(ii)得证
时也成立,综合(i)(ii)得证
方法二:记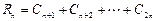 ,
, 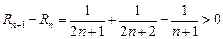
知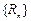 ↑,所以
↑,所以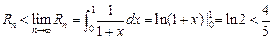
方法三: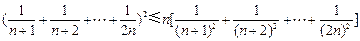
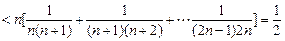
∴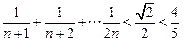
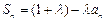 又
又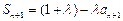 两式相减得
两式相减得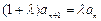
即
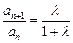 为常数,∴数列
为常数,∴数列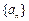 等比.
等比.(2)由(1)知
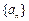 等比,又
等比,又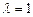 ,当
,当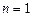 时,
时,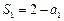 即
即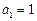
∴
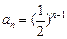 即
即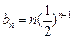
∴
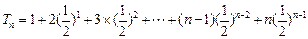
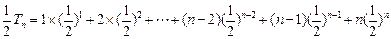
两式相减得
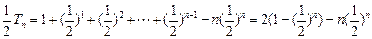
∴
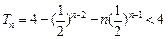 又
又 ∴
∴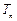 单调递增
单调递增∴当
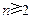 时,
时,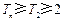 故当
故当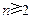 时
时 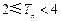
(3)由(1)知
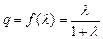 则
则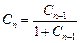 ∴
∴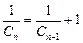
故
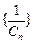 是首项
是首项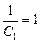 ,公差
,公差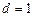 的等差数列. ∴
的等差数列. ∴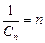 即
即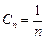
即证:
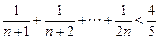
方法一:只须证
 ,用数学归纳法证明(i)当
,用数学归纳法证明(i)当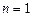 时,左
时,左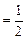 右边
右边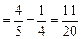 不等式成立,(ii)假设
不等式成立,(ii)假设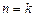 时不等式成立,
时不等式成立,即
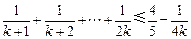 则当
则当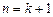 时
时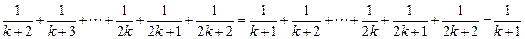
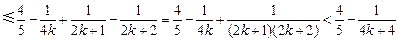
即
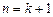 时也成立,综合(i)(ii)得证
时也成立,综合(i)(ii)得证方法二:记
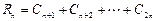 ,
, 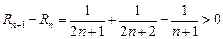
知
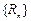 ↑,所以
↑,所以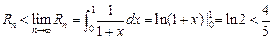
方法三:
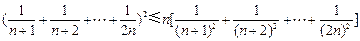
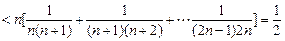
∴
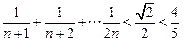

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
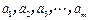 (
(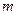 为正整数)满足条件
为正整数)满足条件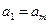 ,
,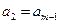 ,…,
,…,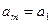 ,即
,即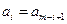 (
(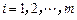 ),我们称其为“对称数列”.
),我们称其为“对称数列”. 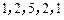 与数列
与数列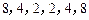 都是“对称数列”.
都是“对称数列”. 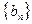 是7项的“对称数列”,其中
是7项的“对称数列”,其中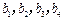 是等差数列,且
是等差数列,且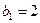 ,
,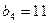 .依次写出
.依次写出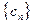 是
是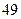 项的“对称数列”,其中
项的“对称数列”,其中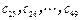 是首项为
是首项为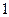 ,公比为
,公比为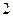 的等比数列,求
的等比数列,求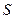 ;
;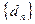 是
是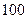 项的“对称数列”,其中
项的“对称数列”,其中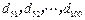 是首项为
是首项为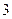 的等差数列.求
的等差数列.求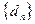 前
前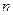 项的和
项的和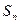
 .
. 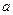 ,计划每年砍伐一些树,且每年砍伐面积的百分比
,计划每年砍伐一些树,且每年砍伐面积的百分比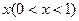 相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面
相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面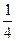 。已知到今年为止,森林剩余面积为原来的
。已知到今年为止,森林剩余面积为原来的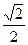 。
。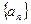 的前
的前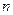 项和为
项和为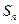 ,且
,且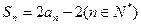 ,数列
,数列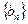 中,
中,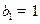 ,
,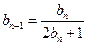 .(
.(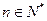 )
)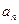 和
和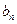
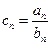 ,求数列
,求数列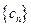 的前n项和
的前n项和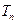 .
.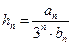 ,若对于一切
,若对于一切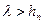 恒成立,求
恒成立,求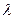 的取值范围
的取值范围 中有
中有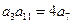 ,数列
,数列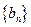 是等差数列,且
是等差数列,且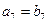 ,则
,则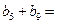 ( )
( )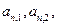 ……
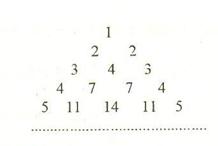
……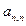 (n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则
(n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则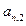 (n
(n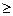 2且n
2且n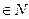 )的表达式
)的表达式
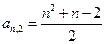
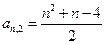
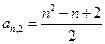
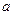 ,
, ,
,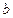 ,
,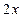 ,则
,则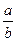 等于( )
等于( )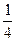
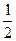
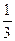
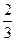
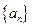 中,
中,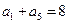 ,
,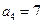 ,则
,则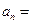 。
。