题目内容
已知数列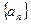 首项
首项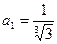 ,公比为
,公比为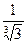 的等比数列,又
的等比数列,又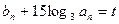 ,常数
,常数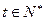 ,数列
,数列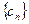 满足
满足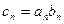 ,
,
(1)、求证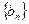 为等差数列;
为等差数列;
(2)、若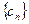 是递减数列,求
是递减数列,求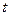 的最小值;(参考数据:
的最小值;(参考数据: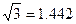 )
)
(3)、是否存在正整数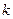 ,使
,使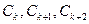 重新排列后成等比数列,若存在,求
重新排列后成等比数列,若存在,求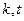 的值,若不存在,说明理由。
的值,若不存在,说明理由。
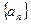 首项
首项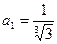 ,公比为
,公比为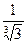 的等比数列,又
的等比数列,又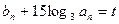 ,常数
,常数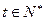 ,数列
,数列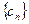 满足
满足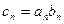 ,
,(1)、求证
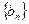 为等差数列;
为等差数列;(2)、若
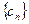 是递减数列,求
是递减数列,求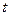 的最小值;(参考数据:
的最小值;(参考数据: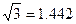 )
)(3)、是否存在正整数
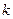 ,使
,使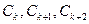 重新排列后成等比数列,若存在,求
重新排列后成等比数列,若存在,求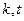 的值,若不存在,说明理由。
的值,若不存在,说明理由。解:(1)由题意知, ,………………………………………
,……………………………………… …1分
…1分
因为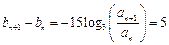 ,
,
∴数列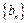 是首项为
是首项为 ,公差
,公差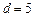 的等差数列.………………4分
的等差数列.………………4分
(2)由(1)知, ,
, ,
,
 恒成立,即
恒成立,即 恒成立,…………6分
恒成立,…………6分
因为 是递减函数,
是递减函数,
所以,当n=1时取最大值, ,……(
,……(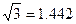 )
)
因而 ,因为
,因为 ,所以
,所以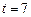 .………………………………………………………8分
.………………………………………………………8分
(3)记 ,
,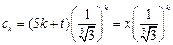 ,
,
 ,
, .9分
.9分
①、若 是等比中项,则由
是等比中项,则由 得
得
化简得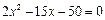 ,解得
,解得 或
或 (舍),
(舍),
所以 ,因而
,因而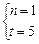 及
及  .………11分
.………11分
②、若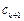 是等比中项,则由
是等比中项,则由 得
得
 化简得
化简得
 ,显然不成立………13分
,显然不成立………13分
③、若 是等比中项,则由
是等比中项,则由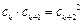
得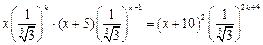
化简得 ,因为
,因为 不是完全不方数,
不是完全不方数,
因而,x的值是无理数,显然不成立.……15分
综上:存在 适合题意。………16分
适合题意。………16分
 ,………………………………………
,……………………………………… …1分
…1分因为
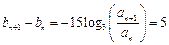 ,
,
∴数列
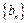 是首项为
是首项为 ,公差
,公差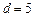 的等差数列.………………4分
的等差数列.………………4分(2)由(1)知,
 ,
, ,
, 恒成立,即
恒成立,即 恒成立,…………6分
恒成立,…………6分因为
 是递减函数,
是递减函数,所以,当n=1时取最大值,
 ,……(
,……(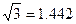 )
)因而
 ,因为
,因为 ,所以
,所以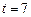 .………………………………………………………8分
.………………………………………………………8分(3)记
 ,
,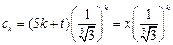 ,
, ,
, .9分
.9分①、若
 是等比中项,则由
是等比中项,则由 得
得
化简得
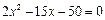 ,解得
,解得 或
或 (舍),
(舍),所以
 ,因而
,因而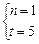 及
及  .………11分
.………11分②、若
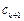 是等比中项,则由
是等比中项,则由 得
得 化简得
化简得 ,显然不成立………13分
,显然不成立………13分③、若
 是等比中项,则由
是等比中项,则由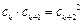
得
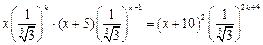
化简得
 ,因为
,因为 不是完全不方数,
不是完全不方数,因而,x的值是无理数,显然不成立.……15分
综上:存在
 适合题意。………16分
适合题意。………16分略

练习册系列答案
相关题目
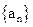 中,
中,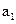 =0,且对任意k
=0,且对任意k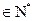 ,
,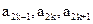 成等差数列,其公差为2k. (Ⅰ)证明
成等差数列,其公差为2k. (Ⅰ)证明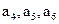 成等比数列;
成等比数列;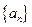 的通项公式;
的通项公式; 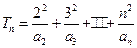 . 证明: 当
. 证明: 当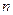 为偶数时, 有
为偶数时, 有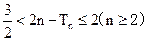 .
. 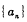 的前n项和为
的前n项和为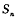 ,对一切
,对一切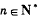 ,点(
,点(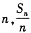 )都在函数
)都在函数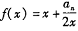 的图象上.
的图象上.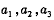 的值,猜想
的值,猜想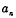 的表达式,并证明你的猜想;
的表达式,并证明你的猜想;
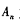 为数列
为数列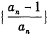 的前项积,是否存在实数、使得不等式
的前项积,是否存在实数、使得不等式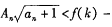
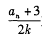 对一切
对一切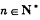 都成立?若存在,求出k的取值范围,若不存在,说明理由.
都成立?若存在,求出k的取值范围,若不存在,说明理由.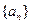 满足
满足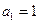 ,
,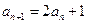 ,则数列
,则数列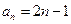
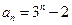
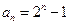
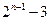
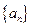 的前n项和为
的前n项和为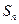 ,若
,若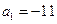 ,
,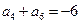 ,则当
,则当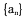 的前n项和为
的前n项和为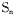 .若,
.若,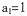
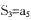 ,
,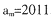 .则m=
.则m=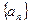 满足a1=2,
满足a1=2,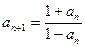 (
(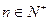 ),则
),则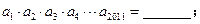
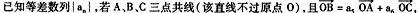

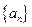 是公差不为零的等差数列,前
是公差不为零的等差数列,前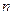 项和为
项和为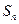 ,满足
,满足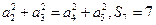 ,则使得
,则使得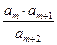 为数列
为数列 的值为
的值为