题目内容
选修4—1:几何证明选讲(10分):
如图:如图E、F、G、H为凸四边形ABCD中AC、BD、AD、DC的中点,∠ABC=∠ADC。

(1)求证:∠ADC=∠GEH; (3分)
(2)求证:E、F、G、H四点共圆; (4分)
(3)求证:∠AEF=∠ACB-∠ACD (3分)
【答案】
证明略
【解析】证明:
(1)因为E、G、H为凸四边形ABCD中AC、AD、DC的中点,
所以EG//CD ,EH//AD 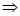 四边形EGDH是平行四边形
四边形EGDH是平行四边形
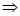 ∠ADC=∠GEH;
--------------3分
∠ADC=∠GEH;
--------------3分
(2)E、F、H为凸四边形ABCD中AC、BD、CD的中点,
FG//AB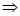 ∠GFD=∠ABD 同理可证∠DBC=∠DFH
∠GFD=∠ABD 同理可证∠DBC=∠DFH
所以∠GFH=∠ABC (FG//AB,FH//BC利用等角定理亦可得) ------5分
又因为∠ABC=∠ADC(条件),∠ADC=∠GEH(已证)
所以 ∠GFH=∠GEH,所以E、F、G、H四点共圆; ---------7分
(3)BC//FH,GH//AC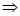 ∠ABC=∠FHG
∠ABC=∠FHG (等角定理)
(等角定理)
E、F、G、H四点共圆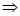 ∠FHG=∠FEG 所以∠ABC=∠FEG
∠FHG=∠FEG 所以∠ABC=∠FEG
EG//CD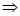 ∠AEG=∠ACD
∠AEG=∠ACD
∠AEF=∠FEG-∠AEG=∠ACB-∠ACD --------10分

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲