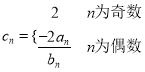题目内容
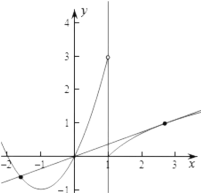
【题目】已知函数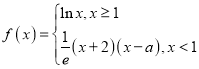 (
(![]() 为常数,
为常数,![]() 为自然对数的底数)的图象在点
为自然对数的底数)的图象在点![]() 处的切线与该函数的图象恰好有三个公共点,则实数
处的切线与该函数的图象恰好有三个公共点,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
【答案】D
【解析】
利用导数的额几何意义求出切线方程,根据分段函数![]() 图象与切线恰好有三个公共点,得到当
图象与切线恰好有三个公共点,得到当![]() 时,切线与
时,切线与![]() 有两个不同的交点,利用二次函数根的分布建立不等式关系,即可求出实数
有两个不同的交点,利用二次函数根的分布建立不等式关系,即可求出实数![]() 的取值范围.
的取值范围.
解:由![]() ,
,![]() ,得
,得![]() ,则
,则![]() (e)
(e)![]() ,
,
![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,①
,①
由于函数![]() ,
,![]() ②
②
![]() 由①②联立方程组可得:
由①②联立方程组可得: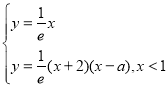 ,
,
化简得:![]() ,③
,③
要使得函数![]() 在点
在点![]() 处的切线与该函数的图象恰好有三个公共点,
处的切线与该函数的图象恰好有三个公共点,
![]() 切线与
切线与![]() ,
,![]() ,在
,在![]() 点有一个交点,
点有一个交点,
![]() 只需要满足③式
只需要满足③式![]() 在
在![]() 内有两个不相同的实数根即可,
内有两个不相同的实数根即可,
则只需![]() 和抛物线对称轴小于1,且当
和抛物线对称轴小于1,且当![]() 时
时![]() ,
,
才能保证在![]() 内有两个不相同的实数根,
内有两个不相同的实数根,
则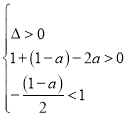 ,即
,即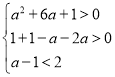 ,
,
解得: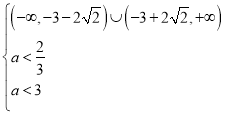 ,
,
![]()
![]() 的范围:
的范围:![]() 或
或![]() .
.
故选:D.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】某农科院为试验冬季昼夜温差对反季节大豆新品种发芽的影响,对温差与发芽率之间的关系进行统计分析研究,记录了6天昼夜温差与实验室中种子发芽数的数据如下:
日期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 | 1月5日 | 1月6日 |
温差 | 10 | 11 | 12 | 13 | 8 | 9 |
发芽数 | 26 | 27 | 30 | 32 | 21 | 24 |
他们确定的方案是先从这6组数据中选出2组,用剩下的4组数据求回归方程,再用选取的两组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若由线性回归方程得到的估计数据与实际数据的误差不超过1粒,则认为得到的线性回归方程是可靠的.请根据1月2,3,4,5日的数据求出![]() 关于
关于![]() 的线性回归方程(保留两位小数),并检验此方程是否可靠.
的线性回归方程(保留两位小数),并检验此方程是否可靠.
参考公式: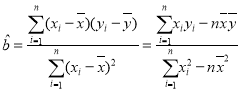 ,
,![]()