题目内容
(12分)已知在数列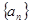 中,
中,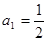 ,
,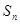 是其前
是其前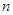 项和,且
项和,且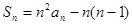
(I)求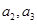 ;(II)证明:数列
;(II)证明:数列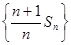 是等差数列;
是等差数列;
(III)令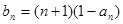 ,记数列
,记数列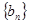 的前
的前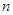 项和为
项和为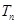 .求证:当
.求证:当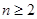 时,
时, 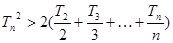 。
。
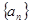 中,
中,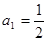 ,
,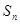 是其前
是其前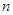 项和,且
项和,且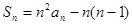
(I)求
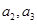 ;(II)证明:数列
;(II)证明:数列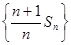 是等差数列;
是等差数列;(III)令
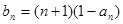 ,记数列
,记数列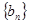 的前
的前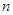 项和为
项和为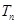 .求证:当
.求证:当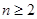 时,
时, 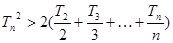 。
。(I)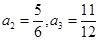 ;(II)见解析; (III)见解析.
;(II)见解析; (III)见解析.
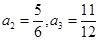 ;(II)见解析; (III)见解析.
;(II)见解析; (III)见解析.(1)令 ,代入
,代入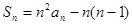 可求出
可求出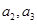 ;
;
(2)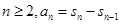 代入
代入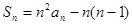 整理得
整理得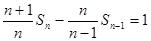 ,所以数列
,所以数列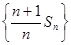 是等差数列;
是等差数列;
(3)由(1),(2)可求得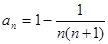 ,
,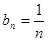 。所以
。所以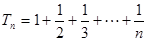 。当
。当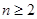 时,
时,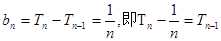 ;两边平方整理得
;两边平方整理得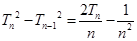 。叠加得
。叠加得
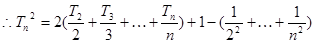 ,放缩求得
,放缩求得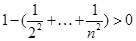 ,即证得结论。
,即证得结论。
(I)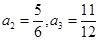 ;
;
(II)由条件可得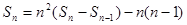 ,
,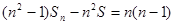
两边同除以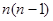 ,得:
,得: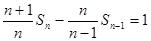
所以:数列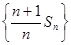 成等差数列,且首项和公差均为1
成等差数列,且首项和公差均为1
(III)由(Ⅰ)可得: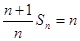 ,
, ,代入
,代入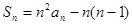 可得
可得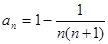 ,所以
,所以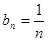 ,
,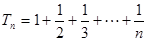 .
.
当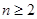 时,
时,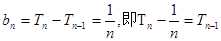
平方则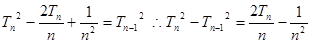
叠加得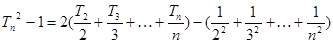
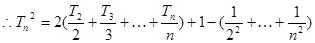
又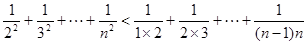
=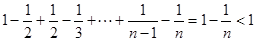
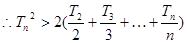
 ,代入
,代入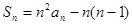 可求出
可求出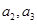 ;
;(2)
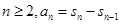 代入
代入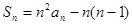 整理得
整理得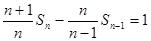 ,所以数列
,所以数列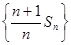 是等差数列;
是等差数列;(3)由(1),(2)可求得
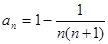 ,
,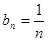 。所以
。所以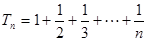 。当
。当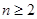 时,
时,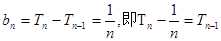 ;两边平方整理得
;两边平方整理得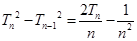 。叠加得
。叠加得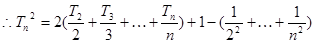 ,放缩求得
,放缩求得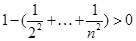 ,即证得结论。
,即证得结论。(I)
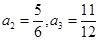 ;
;(II)由条件可得
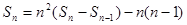 ,
,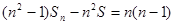
两边同除以
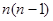 ,得:
,得: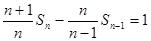
所以:数列
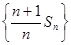 成等差数列,且首项和公差均为1
成等差数列,且首项和公差均为1(III)由(Ⅰ)可得:
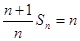 ,
, ,代入
,代入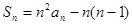 可得
可得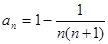 ,所以
,所以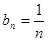 ,
,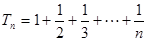 .
.当
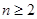 时,
时,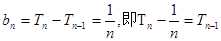
平方则
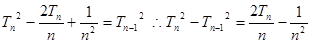
叠加得
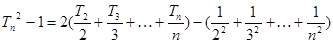
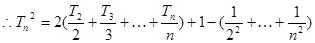
又
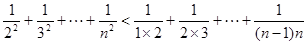
=
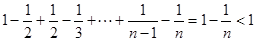
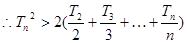

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
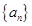 中,
中, 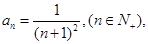 记
记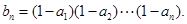
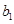 、
、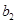 、
、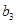 、
、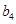 并推测
并推测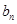 ;
;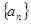 中,
中,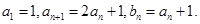
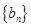 是等比数列;
是等比数列;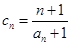 ,求数列
,求数列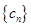 的前
的前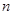 项和
项和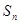

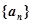 中,
中,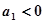 ,又
,又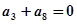 ,则使数列
,则使数列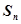 取最小值时的n的值是 。
取最小值时的n的值是 。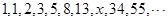 中的
中的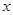 的值为 ▲ .
的值为 ▲ .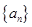 中,
中,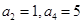 ,则
,则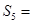

 为等差数列,若
为等差数列,若 ,则
,则 的值为( )
的值为( )
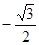
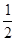

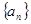 是等差数列,首项
是等差数列,首项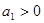 ,且
,且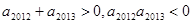 ,则使前n项和Sn>0成立的最大自然数n是( )
,则使前n项和Sn>0成立的最大自然数n是( )