题目内容
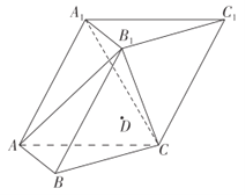
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,已知
是边长为2的正三角形,已知![]() 点满足
点满足![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)求异面直线![]() 与
与![]() 的距离;
的距离;
(3)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面?若存在,请确定点
平面?若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在点
(3)存在点![]() ,其坐标为
,其坐标为![]() ,即恰好为
,即恰好为![]() 点
点
【解析】
(1)建立空间直角坐标系,利用平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值,由此求得其大小.
的余弦值,由此求得其大小.
(2)求得异面直线![]() 与
与![]() 的公垂线的方向向量,并由此计算出异面直线
的公垂线的方向向量,并由此计算出异面直线![]() 与
与![]() 的距离.
的距离.
(3)根据![]() 求得
求得![]() 点的坐标,设出
点的坐标,设出![]() 点的坐标,根据
点的坐标,根据![]() 、
、![]() 与平面
与平面![]() 的法向量垂直列方程组,解方程组求得
的法向量垂直列方程组,解方程组求得![]() 点的坐标,由此判断出存在
点的坐标,由此判断出存在![]() 点符合题意.
点符合题意.
(1)![]() 侧面
侧面![]() 底面
底面![]() ,又
,又![]() 均为正三角形,取
均为正三角形,取![]() 得中点
得中点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() 底面
底面![]() ,
,![]()
故以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立
轴建立![]() 如图所示空间直角坐标系,
如图所示空间直角坐标系,
则![]()
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]()
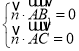
取![]() ,可得
,可得![]()
又平面![]() 的一个法向量为
的一个法向量为![]()
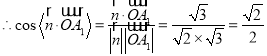
由图知二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的大小为
的大小为![]() .
.
(2)异面直线![]() 与
与![]() 的公垂线的方向向量
的公垂线的方向向量![]() ,则
,则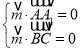
易得![]() ,异面直线
,异面直线![]() 与
与![]() 的距离
的距离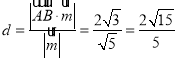
(3)![]() ,而
,而![]()
![]()
又![]() ,
,![]() 点
点![]() 的坐标为
的坐标为![]()
假设存在点![]() 符合题意,则点
符合题意,则点![]() 的坐标可设为
的坐标可设为![]()
![]()
![]() 平面
平面![]()
![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
![]() 由
由![]() ,得
,得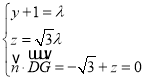
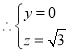 .
.
又![]() 平面
平面![]() ,
,
故存在点![]() ,使
,使![]() 平面
平面![]() ,其坐标为
,其坐标为![]() ,即恰好为
,即恰好为![]() 点.
点.

【题目】根据国家统计局数据,1978年至2018年我国GDP总量从0.37万亿元跃升至90万亿元,实际增长了242倍多,综合国力大幅提升.
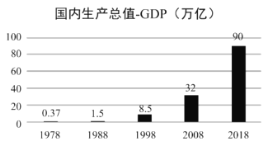
将年份1978,1988,1998,2008,2018分别用1,2,3,4,5代替,并表示为![]() ;
;![]() 表示全国GDP总量,表中
表示全国GDP总量,表中![]() ,
,![]() .
.
|
|
|
|
|
|
3 | 26.474 | 1.903 | 10 | 209.76 | 14.05 |
(1)根据数据及统计图表,判断![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为全国GDP总量
为自然对数的底数)哪一个更适宜作为全国GDP总量![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由),并求出
的回归方程类型?(给出判断即可,不必说明理由),并求出![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)使用参考数据,估计2020年的全国GDP总量.
线性回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
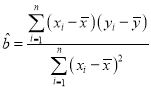 ,
,![]() .
.
参考数据:
| 4 | 5 | 6 | 7 | 8 |
| 55 | 148 | 403 | 1097 | 2981 |