题目内容
已知函数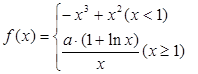 ,曲线
,曲线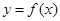 上是否存在两点
上是否存在两点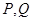 ,使得△
,使得△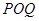 是以
是以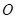 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在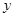 轴上.如果存在,求出实数
轴上.如果存在,求出实数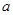 的范围;如果不存在,说明理由.
的范围;如果不存在,说明理由.
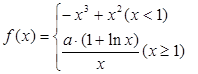 ,曲线
,曲线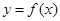 上是否存在两点
上是否存在两点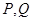 ,使得△
,使得△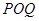 是以
是以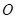 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在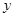 轴上.如果存在,求出实数
轴上.如果存在,求出实数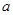 的范围;如果不存在,说明理由.
的范围;如果不存在,说明理由.存在,且实数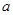 的取值范围是
的取值范围是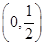 .
.
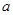 的取值范围是
的取值范围是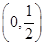 .
.试题分析:先将斜边
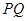 的中点在
的中点在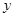 轴上这一条件进行转化,确定点
轴上这一条件进行转化,确定点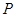 与点
与点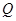 之间的关系,并将
之间的关系,并将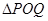 是以点
是以点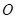 为直角顶点条件转化为
为直角顶点条件转化为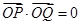 ,进行得到一个方程,然后就这个方程在定义域上是否有解对自变量的取值进行分类讨论,进而求出参数
,进行得到一个方程,然后就这个方程在定义域上是否有解对自变量的取值进行分类讨论,进而求出参数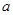 的取值范围.
的取值范围.试题解析:假设曲线
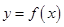 上存在两点
上存在两点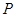 、
、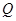 满足题意,则
满足题意,则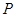 、
、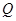 两点只能在
两点只能在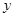 轴两侧,
轴两侧,因为
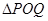 是以
是以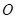 为直角顶点的直角三角形,所以
为直角顶点的直角三角形,所以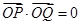 ,
,不妨设
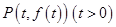 ,则由
,则由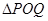 的斜边的中点在
的斜边的中点在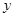 轴上知
轴上知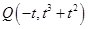 ,且
,且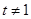 ,
,由
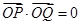 ,所以
,所以 (*)
(*)是否存在两点
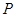 、
、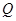 满足题意等价于方程(*)是否有解问题,
满足题意等价于方程(*)是否有解问题,(1)当
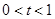 时,即
时,即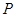 、
、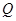 都在
都在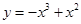 上,则
上,则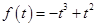 ,
,代入方程(*),得
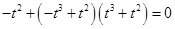 ,即
,即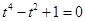 ,而此方程无实数解;
,而此方程无实数解;(2)当
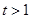 时,即
时,即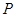 在
在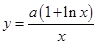 上,
上,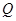 在
在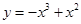 上,
上,则
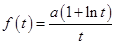 ,代入方程(*)得,
,代入方程(*)得,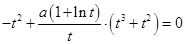 ,即
,即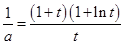 ,
,设
 ,则
,则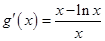 ,
,再设
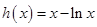 ,则
,则 ,所以
,所以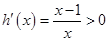 在
在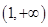 上恒成立,
上恒成立,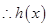 在
在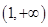 上单调递增,
上单调递增, ,从而
,从而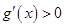 ,故
,故 在
在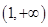 上也单调递增,
上也单调递增,所以
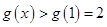 ,即
,即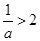 ,解得
,解得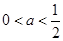 ,
,即当
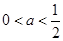 时,方程
时,方程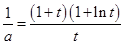 有解,即方程(*)有解,
有解,即方程(*)有解,所以曲线
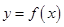 上总存在两点
上总存在两点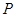 、
、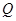 ,使得
,使得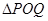 是以
是以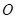 为直角顶点的直角三角形,
为直角顶点的直角三角形,且此三角形斜边的中点在
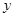 轴上,此时
轴上,此时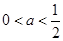 .
.
练习册系列答案
相关题目
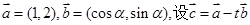 (
(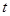 为实数).
为实数).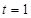 时,若
时,若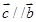 ,求
,求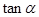 ;
;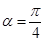 ,求
,求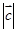 的最小值,并求出此时向量
的最小值,并求出此时向量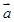 在
在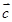 方向上的投影.
方向上的投影.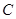 的圆心
的圆心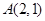 关于直线
关于直线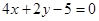 对称,圆
对称,圆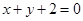 相切.
相切.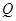 为圆
为圆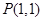 ,
,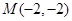 ,求
,求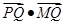 的最小值;
的最小值;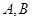 ,且直线
,且直线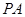 和直线
和直线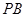 的倾斜角互补,
的倾斜角互补,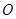 为坐标原点,试判断直线
为坐标原点,试判断直线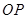 和
和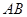 是否平行?请说明理由.
是否平行?请说明理由.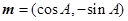 ,
,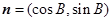 ,
,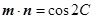 ,其中
,其中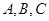 为
为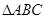 的内角.
的内角.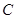 的大小;
的大小;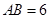 ,且
,且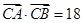 ,求
,求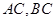 的长.
的长.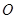 为
为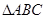 内一点,若对任意
内一点,若对任意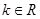 ,恒有
,恒有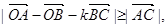 则
则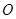 是
是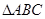 的三边中垂线的交点,
的三边中垂线的交点,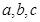 分别为角
分别为角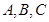 对应的边,已知
对应的边,已知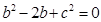 ,则
,则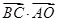 的范围是_____________.
的范围是_____________.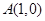 和点
和点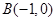 ,
,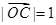 ,且
,且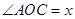 ,其中
,其中 为坐标原点.
为坐标原点.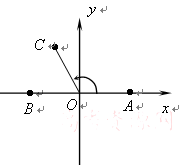
 ,设点
,设点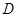 为线段
为线段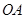 上的动点,求
上的动点,求 的最小值;
的最小值;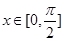 ,向量
,向量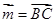 ,
,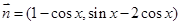 ,求
,求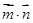 的最小值及对应的
的最小值及对应的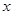 值.
值.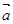 、
、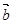 、
、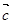 是同一平面的三个单位向量,且
是同一平面的三个单位向量,且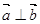 , 则
, 则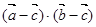 的最小值为( )
的最小值为( )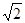
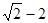
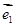 和
和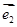 是平面上的两个单位向量,且
是平面上的两个单位向量,且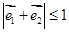 ,
,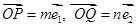 ,若O为坐标原点,
,若O为坐标原点,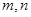 均为正常数,则
均为正常数,则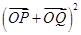 的最大值为 ( )
的最大值为 ( )


