题目内容
17.已知数列{an}满足:an+1=f(an),n∈N*.(1)f(x)=x-sinx,0<a1<1,求证:0<an+1<an<1;
(2)f(x)=x3-x2+$\frac{x}{2}$+$\frac{1}{4}$,试确定一个首项a1,使得数列{an}为单调数列,并证明你的结论;
(3)f(x)=$\frac{1}{4}$(x2+3),a1>0,若对一切n∈N*,都有an+1>an,求a1的取值范围.
分析 (1)求导f′(x)=1-cosx≥0,从而可得函数f(x)是增函数,从而利用数学归纳法证明;
(2)当a1=0时,可得数列{an}为单调递增数列,再利用(1)中的方法证明即可;
(3)结合(1),根据f(x)=$\frac{1}{4}$(x2+3)在(0,+∞)上是增函数,从而只需使a2>a1,从而解得.
解答 证明:(1)∵f(x)=x-sinx,∴f′(x)=1-cosx≥0,
∴函数f(x)是增函数,
当n=1时,∵0<a1<1,
∴a2=f(a1)=a1-sina1<a1,
∴0<a2<a1,
假设n=k时命题成立,即0<ak+1<ak<1;
当设n=k+1时,
∵函数f(x)是增函数,
即f(0)<f(ak+1)<f(ak)<1;
即0<ak+2<ak+1<1;
综上所述,0<an+1<an<1.
(2)当a1=0时,可得数列{an}为单调递增数列,证明如下:
∵f(x)=x3-x2+$\frac{x}{2}$+$\frac{1}{4}$,
∴f′(x)=3x2-2x+$\frac{1}{2}$,
∵△=4-4×3×$\frac{1}{2}$<0,
∴函数f(x)是增函数,
当n=1时,a1=0,a2=$\frac{1}{4}$,故a1<a2,
假设当n=k时,ak<ak+1;
当n=k+1时,∵函数f(x)是增函数,
∴f(ak)<f(ak+1),
即ak+1<ak+2;
综上所述,对一切n∈N*,都有an+1>an.
故数列{an}为单调递增数列.
(3)∵f(x)=$\frac{1}{4}$(x2+3)在(0,+∞)上是增函数,
∴若使对一切n∈N*,都有an+1>an,
只需使a2>a1,
∵a2=$\frac{1}{4}$(a12+3),
∴a2-a1=$\frac{1}{4}$(a12+3)-a1=$\frac{({a}_{1}-1)({a}_{1}-3)}{4}$,
∴a1<1或a1>3,
又∵a1>0,
∴0<a1<1或a1>3.
点评 本题考查了导数的综合应用及数列的应用,同时考查了数学归纳法的应用.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | $\frac{9}{16}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{9}{8}$ |
| A. | 1 | B. | 17 | C. | 23 | D. | 37 |
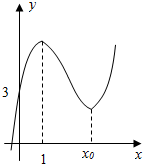 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.