题目内容
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,双曲线E的参数方程为  (θ为参数),设E的右焦点为F,经过第一象限的渐进线为l.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(θ为参数),设E的右焦点为F,经过第一象限的渐进线为l.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l的极坐标方程;
(2)设过F与l垂直的直线与y轴相交于点A,P是l上异于原点O的点,当A,O,F,P四点在同一圆上时,求这个圆的极坐标方程及点P的极坐标.
【答案】
(1)解:∵双曲线E的参数方程为 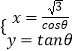 (θ为参数),
(θ为参数),
∴ ![]() ,
, ![]() ,
,
∴ ![]() =
= ![]() =1,
=1,
∴双曲线E的普通方程为 ![]() .
.
∴直线l在直角坐标系中的方程为y= ![]() ,其过原点,倾斜角为
,其过原点,倾斜角为 ![]() ,
,
∴l的极坐标方程为 ![]() .
.
(2)解:由题意A、O、F、P四点共圆等价于P是点A,O,F确定的圆(记为圆C,C为圆心)与直线l的交点(异于原点O),
∵AO⊥OF,∴线段AF为圆C的直径,
由(Ⅰ)知,|OF|=2,
又A是过F与l垂直的直线与y轴的交点,
∴∠AFO= ![]() ,|AF|=4,
,|AF|=4,
于是圆C的半径为2,圆心的极坐标为(2, ![]() ),
),
∴圆C的极坐标方程为 ![]() ,
,
此时,点P的极坐标为(4cos( ![]() ),
), ![]() ),即(2
),即(2 ![]() ,
, ![]() ).
).
【解析】(1)由双曲线E的参数方程求出双曲线E的普通方程为 ![]() .从而求出直线l在直角坐标系中的方程,由此能求出l的极坐标方程.(2)由题意A、O、F、P四点共圆等价于P是点A,O,F确定的圆(记为圆C,C为圆心)与直线l的交点(异于原点O),线段AF为圆C的直径,A是过F与l垂直的直线与y轴的交点,从而C的半径为2,圆心的极坐标为(2,
.从而求出直线l在直角坐标系中的方程,由此能求出l的极坐标方程.(2)由题意A、O、F、P四点共圆等价于P是点A,O,F确定的圆(记为圆C,C为圆心)与直线l的交点(异于原点O),线段AF为圆C的直径,A是过F与l垂直的直线与y轴的交点,从而C的半径为2,圆心的极坐标为(2, ![]() ),由此能求出点P的极坐标.
),由此能求出点P的极坐标.

练习册系列答案
相关题目
