题目内容
(本小题满分10分)已知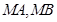 是曲线
是曲线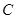 :
: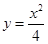 的两条切线,其中
的两条切线,其中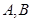 是切点,
是切点,
(I)求证: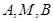 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(II)若直线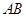 过曲线
过曲线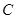 的焦点
的焦点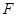 ,求
,求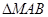 面积的最小值;
面积的最小值;
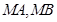 是曲线
是曲线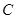 :
: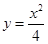 的两条切线,其中
的两条切线,其中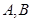 是切点,
是切点,(I)求证:
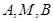 三点的横坐标成等差数列;
三点的横坐标成等差数列;(II)若直线
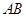 过曲线
过曲线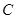 的焦点
的焦点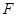 ,求
,求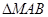 面积的最小值;
面积的最小值; (1)证明:见解析;(2)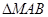 面积的最小值为
面积的最小值为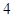 。
。
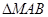 面积的最小值为
面积的最小值为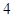 。
。(I)设 、
、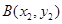 ,
, ,再利用导数求出切线MA、MB的方程.然后两方程联立解出交点M的横坐标为
,再利用导数求出切线MA、MB的方程.然后两方程联立解出交点M的横坐标为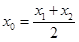 即可.
即可.
(II) 焦点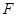 的坐标为(0,1),显然直线
的坐标为(0,1),显然直线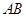 的斜率是存在的;
的斜率是存在的;
设直线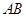 的方程为
的方程为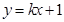 它与抛物线方程联立,消y后得关于x的一元二次方程,再根据弦长公式得
它与抛物线方程联立,消y后得关于x的一元二次方程,再根据弦长公式得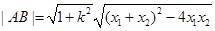 和点到直线的距离公式得到面积S关于k的函数关系式,然后再利用函数求最值的方法求最值.
和点到直线的距离公式得到面积S关于k的函数关系式,然后再利用函数求最值的方法求最值.
(1)证明: ,设
,设 、
、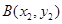 ;
;
直线 的方程为
的方程为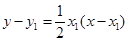 ① 直线
① 直线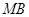 的方程为
的方程为 ②
②
①-②得:点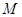 的横坐标
的横坐标 ,所以 点
,所以 点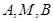 的横坐标成等差数列;…4分
的横坐标成等差数列;…4分
(2)焦点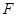 的坐标为(0,1),显然直线
的坐标为(0,1),显然直线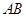 的斜率是存在的;
的斜率是存在的;
设直线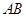 的方程为
的方程为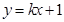
将直线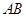 的方程代入
的方程代入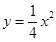 得:
得: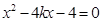 (
(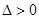 恒成立)
恒成立)
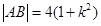 ,且
,且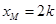 又由①②得:
又由①②得:
,从而点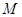 到直线
到直线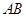 的距离
的距离 , …8分
, …8分
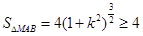 当且仅当
当且仅当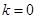 时取等号;
时取等号;
故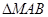 面积的最小值为
面积的最小值为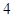 …10分
…10分
 、
、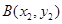 ,
, ,再利用导数求出切线MA、MB的方程.然后两方程联立解出交点M的横坐标为
,再利用导数求出切线MA、MB的方程.然后两方程联立解出交点M的横坐标为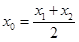 即可.
即可.(II) 焦点
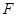 的坐标为(0,1),显然直线
的坐标为(0,1),显然直线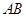 的斜率是存在的;
的斜率是存在的;设直线
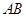 的方程为
的方程为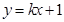 它与抛物线方程联立,消y后得关于x的一元二次方程,再根据弦长公式得
它与抛物线方程联立,消y后得关于x的一元二次方程,再根据弦长公式得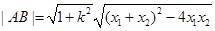 和点到直线的距离公式得到面积S关于k的函数关系式,然后再利用函数求最值的方法求最值.
和点到直线的距离公式得到面积S关于k的函数关系式,然后再利用函数求最值的方法求最值.(1)证明:
 ,设
,设 、
、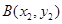 ;
;直线
 的方程为
的方程为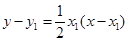 ① 直线
① 直线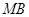 的方程为
的方程为 ②
②①-②得:点
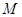 的横坐标
的横坐标 ,所以 点
,所以 点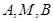 的横坐标成等差数列;…4分
的横坐标成等差数列;…4分(2)焦点
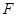 的坐标为(0,1),显然直线
的坐标为(0,1),显然直线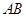 的斜率是存在的;
的斜率是存在的;设直线
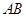 的方程为
的方程为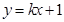
将直线
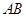 的方程代入
的方程代入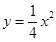 得:
得: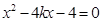 (
(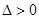 恒成立)
恒成立)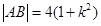 ,且
,且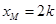 又由①②得:
又由①②得:
,从而点
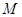 到直线
到直线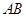 的距离
的距离 , …8分
, …8分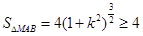 当且仅当
当且仅当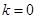 时取等号;
时取等号;故
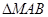 面积的最小值为
面积的最小值为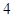 …10分
…10分
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
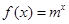 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).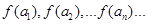 (n∈
(n∈ ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.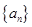 是等差数列;
是等差数列; 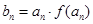 ,且数列
,且数列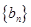 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;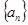 中,已知
中,已知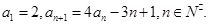
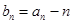 ,求证:数列
,求证:数列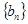 是等比数列;
是等比数列;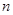 项和
项和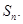
 中,
中,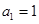 ,
,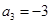 .
. 项和
项和 ,求
,求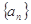 中,若
中,若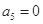 ,则有等式
,则有等式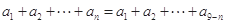
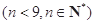 成立.类比上述性质:在等比数列
成立.类比上述性质:在等比数列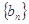 中,若
中,若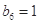 ,则有等式 成立.
,则有等式 成立.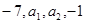 四个实数成等差数列,-4,b1,b2,b3,-1五个实数成等比数列,则
四个实数成等差数列,-4,b1,b2,b3,-1五个实数成等比数列,则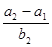 = ( )
= ( ) 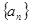 的前
的前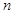 项和
项和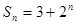 ,则数列
,则数列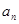 }是等差数列,
}是等差数列,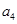 =7,则
=7,则 =_________
=_________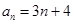 ,则数列{an}是公差为 的等差数列.
,则数列{an}是公差为 的等差数列.